已知Rt△ABC,∠B=90°，直线EF分别于两直角边AB、AC交于E、F两点，且EF//AC。P是斜边AC的中点，连接PE、PF，且已知AB=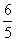
,BC=
。
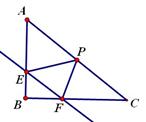
（1） 如图1，当E、F均为两直角边中点时，求证：四边形EPFB是矩形，并求出此时EF的长。
（2） 如图2，设EF的长度为x（x>0）,当sin∠EPF=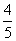
（∠EPF为锐角）时，用含x的代数式表示EP的长度。
（3） 记△PEF 的面积为S，则当EP为多少时，S的值最大，并求出该最大值。
考前必练系列答案科目：初中数学 来源： 题型：
为了节约资源，科学指导居民改善居住条件，小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积（平方米） | 单 |
| 不超过30（平方米） | 0.3 |
| 超过30平方米不超过 | 0.5 |
| 超过 | 0.7 |
根据这个购房方案：
⑴若某三口之家欲购买120平方米的商品房，求其应缴纳的房款；
⑵设该家庭购买商品房的人均面积为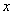
平方米，缴纳房款y万元，请求出
关于x的
函数关系式；
⑶若该家庭购买商品房的人均面积为50平方米，缴纳房款为y万元，且 57<y≤60 时，
求
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
亲爱的同学，你能比较20092010和20102009的大小吗？为了解决这个问题，我们先把它抽象成数学问题，写出它的一般形式，即比较nn+1和（n+1）n的大小（n是自然数）然后，我们分析n=1,n=2,n=3…这些简单情形入手，从中发现规律，经过归纳、猜想，得出结论。
(1)通过计算，比较下列各组中两个数的大小（在空格中选填 ﹤﹥﹦ 号）
12 ﹤ 21 23 ﹤ 32 34 ﹤ 43 45 ﹤ 54 56 ﹤ 65…
(2)从第（1）小题的结果，经过归纳，可以猜想出nn+1和（n+1）n的大小关系是
（3）根据上面归纳猜想得到的一般结论，试比较下列两个数的大小：20102011 20112010
查看答案和解析>>
科目：初中数学 来源： 题型：
某校对初三（2）班40名学生体育考试中“立定跳远”项目的得分情况进行了统计，结果如下表，
| 得 分 | 10分 | 9分 | 8分 | 7分 | 6分以下 |
| 人数（人） | 20 | 12 | 5 | 2 | 1 |
根据表中数据，若随机抽取该班的一名学生，则该学生“立定跳远”得分恰好是10分的概率是 。
查看答案和解析>>
科目：初中数学 来源： 题型：
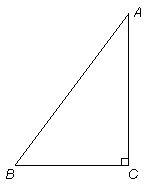
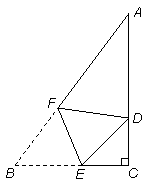
如图，三角形纸片ABC中，∠C＝90°，AC＝4，BC＝3．将纸片折叠，使点B落在AC边上的点D处，折痕与BC、AB分别交于点E、F．
（1）设BE＝x，DC＝y，求y关于x的函数关系式，并确定自变量x的取值范围；
（2）当△ADF是直角三角形时，求BE的长；
（3）当△ADF是等腰三角形，且∠A是顶角时，求BE的长。
 |  | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
……………矩形 ，EF 
价（万元/平方米）
,②2a-2b ,③ 
中任意选取两个代数式构造分式，然后进行化简，并求当a、b为不等式组
整数解，且a>b时的值。
A．
B．
C．
D．