
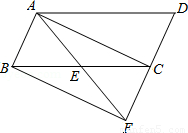
如图,已知E是▱ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE.
(2)连接AC.BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.
(1)、(2)证明见解析
【解析】证明:(1)∵四边形ABCD为平行四边形,∴AB∥DC。∴∠ABE=∠ECF。
又∵E为BC的中点,∴BE=CE。
在△ABE和△FCE中,∵∠ABE=∠FCE,BE=CE,∠AEB=∠FEC,
∴△ABE≌△FCE(ASA)。
(2)∵△ABE≌△FCE,∴AB=CF。
又AB∥CF,∴四边形ABFC为平行四边形。∴BE=EC,AE=EF。
又∵∠AEC=2∠ABC,且∠AEC为△ABE的外角,∴∠AEC=∠ABC+∠EAB。
∴∠ABC=∠EAB,∴AE=BE。∴AE+EF=BE+EC,即AF=BC。
∴四边形ABFC为矩形。
(1)由ABCD为平行四边形,根据平行四边形的对边平行得到AB与DC平行,根据两直线平行内错角相等得到一对角相等,由E为BC的中点,得到两条线段相等,再由对应角相等,利用ASA可得出三角形ABE与三角形FCE全等。
(2)由△ABE≌△FCE,根据全等三角形的对应边相等得到AB=CF;再由AB与CF平行,根据一组对边平行且相等的四边形为平行四边形得到ABFC为平行四边形,根据平行四边形的对角线互相平分得到AE=EF,BE=EC;再由∠AEC为三角形ABE的外角,利用外角的性质得到∠AEB等于∠ABE+∠EAB,再由∠AEC=2∠ABC,得到∠ABE=∠EAB,利用等角对等边可得出AE=BE,可得出AF=BC,利用对角线相等的平行四边形为矩形可得出ABFC为矩形。


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
 如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为
如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB. | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么,| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b+c |
| 3 |
| 3 | abc |
| 3 | abc |
| a+b |
| 2 |
| ab |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com