
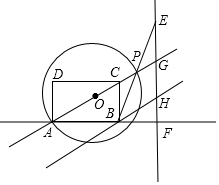
 ��ͼ���ھ���ABCD�У���CAB=30�㣬P��ֱ��AC��һ���㣬����BP���ӳ�����E��ʹBP=PE������E��EF��AB�ڵ�F����ֱ��AC�ڵ�G������B��BH��AC��ֱ��EF�ڵ�H����APΪֱ���ġ�O��ֱ��AB�ڵ�Q��
��ͼ���ھ���ABCD�У���CAB=30�㣬P��ֱ��AC��һ���㣬����BP���ӳ�����E��ʹBP=PE������E��EF��AB�ڵ�F����ֱ��AC�ڵ�G������B��BH��AC��ֱ��EF�ڵ�H����APΪֱ���ġ�O��ֱ��AB�ڵ�Q������ ��1����ͼ1�У����O��AF��M������PM��ֻҪ֤��EF=2PM��AP=2PM�����ɽ�����⣻
��2����ͼ2�У���BN��AC��N����PC=PG=a����AC=3a��BC=$\frac{3a}{2}$��BN=$\frac{3\sqrt{3}}{4}$a�����������ʽ���a���ɽ�����⣻
��3���ٷ�����������ͼ3�У����ı���CGHB������ʱ����ͼ4�У����ı���BCGH������ʱ���ֱ���⼴�ɣ�
�ڷ������������ۣ���O��PB���У���O��BH���У���O��PH���У��ֱ���⼴�ɣ�
��� ��1��֤������ͼ1�У����O��AF��M������PM��
��AP��ֱ����
���AMP=90�㣬
��EF��AB��
���AMP=��AFE=90�㣬
��PM��EF��
��BP=PE��
��BM=MF��
��EF=2PM��
��Rt��APM�У��ߡ�PAM=30�㣬
��AP=2PM��
��AP=EF��
��2���⣺��ͼ2�У���BN��AC��N����PC=PG=a����AC=3a��BC=$\frac{3a}{2}$��BN=$\frac{3\sqrt{3}}{4}$a��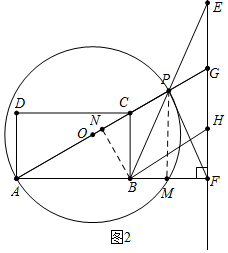
������2a•$\frac{3\sqrt{3}}{4}$a=24$\sqrt{3}$��
���a=4��
��AP=4a=16��
��OA=8��
���O�İ뾶Ϊ8��
��3������ͼ3�У����ı���CGHB������ʱ��
�ߡ�GCB=60�㣬
���CGB�ǵȱ������Σ�
��EG=BC��EG��CB��
���ı���BCEG��ƽ���ı��Σ���BG=BC��
���ı���BCEG�����Σ�
��BE��AC��
��AP=AB•cos30��=6��$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$��
��ͼ4�У����ı���BCGH������ʱ��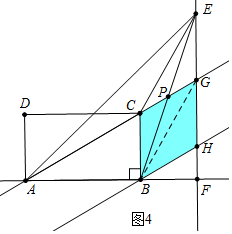
��֪BC=CG=2$\sqrt{3}$��AC=4$\sqrt{3}$��PC=PG=$\sqrt{3}$��
��AP=5$\sqrt{3}$��
��������������������AP��ֵΪ3$\sqrt{3}$��5$\sqrt{3}$��
����ͼ5�У�����O��PB����ʱ��
��֪��BE��AP���ɢٿ�֪��AF=BF=3��FH=BF•tan30��=$\sqrt{3}$��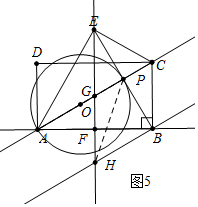
��ͼ6�У�����O��BH����ʱ����֪AP=6��PC=PG=AC-AP=4$\sqrt{3}$-6��
��AG=AP-PG=12-4$\sqrt{3}$��
��AF=AG•cos30��=6$\sqrt{3}$-6��BF=AB-AF=12-6$\sqrt{3}$��
��FH=BF•tan30��=4$\sqrt{3}$-6��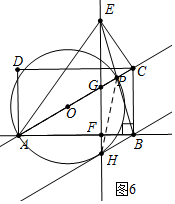
��ͼ7�У�����O��PH����ʱ���ɢٿ�֪��BH=BC=CG=GH=2$\sqrt{3}$��
��FH=$\frac{1}{2}$BH=$\sqrt{3}$��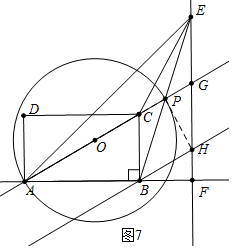
��������������O���BHPijһ�����ڵ�ֱ������ʱ��FH�ij�Ϊ$\sqrt{3}$��4$\sqrt{3}$-6��
���� ���⿼��Բ�ۺ��⡢���ߵ��ж������ʡ����ε����ʡ����ε��ж������ʡ��ȱ������ε��ж������ʡ�������Ǻ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼�������⣬�����п�ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m-1 | B�� | m+1 | C�� | m2-1 | D�� | ��m-1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
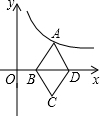 ��ͼ����֪����ABCD�ĶԽ���BD��x���ϣ�A����y=$\frac{k}{x}$��x��0����ͼ���ϣ�C�������Ϊ��2��-1������k=2��
��ͼ����֪����ABCD�ĶԽ���BD��x���ϣ�A����y=$\frac{k}{x}$��x��0����ͼ���ϣ�C�������Ϊ��2��-1������k=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
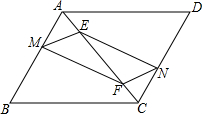 ��ͼ����?ABCD�У�M��N�ֱ���AB��CD�ϵĵ㣬AM=CN��E��F��AC�ϵĵ㣬AE=CF����֤���ı���MENF��ƽ���ı��Σ�
��ͼ����?ABCD�У�M��N�ֱ���AB��CD�ϵĵ㣬AM=CN��E��F��AC�ϵĵ㣬AE=CF����֤���ı���MENF��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�ĶԽ����ཻ�ڵ�O���Խ���AC=6��BD=8����E��BC���ӳ����ϣ���OE=OB������DE��
��ͼ������ABCD�ĶԽ����ཻ�ڵ�O���Խ���AC=6��BD=8����E��BC���ӳ����ϣ���OE=OB������DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
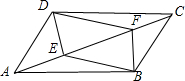 ��֪����ͼ���ı���DEBF��ƽ���ı��Σ���AE=CF��
��֪����ͼ���ı���DEBF��ƽ���ı��Σ���AE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
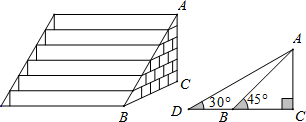
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
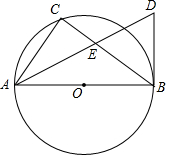 ��ͼ��AB�ǡ�Oֱ������C�ڡ�O�ϣ�ADƽ�֡�CAB��BD�ǡ�O�����ߣ�AD��BC�ཻ�ڵ�E��
��ͼ��AB�ǡ�Oֱ������C�ڡ�O�ϣ�ADƽ�֡�CAB��BD�ǡ�O�����ߣ�AD��BC�ཻ�ڵ�E���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com