
分析 (1)根据题意可以列出相应的方程,从而可以解答本题;
(2)根据(1)中的答案可以解答本题;
(3)根据题意可以得到利润W与降价之间的函数关系式,从而可以解答本题.
解答 解:(1)设每千克核桃应降价x元,
(60-x-40)(100+$\frac{x}{2}×20$)=2240,
解得,x1=4,x2=6,
即每千克核桃应降价4元或6元;
(2)由(1)可知每千克核桃可降价4元或6元,
∵要尽可能让利于顾客,
∴每千克核桃应降价6元,此时售价为:60-6=54(元),
∴$\frac{54}{60}×10$=9,
即该店应按原价的九折出售;
(3)设每千克应降价y元,
W=(60-y-40)(100+$\frac{y}{2}×20$)=-10(y-5)2+2250,
∴当y=5时,W取得最大值,此时W=2250,
∴60-y=60-5=55,
即该专卖店想获得最大利润W,核桃的单价应定为55元,最大利润是2250元.
点评 本题考查二次函数的应用、一元二次方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的顶点式求函数的最值,注意(2)尽可能让利于顾客.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
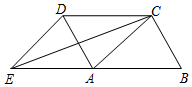 如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是( )
如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是( )| A. | AB=AD | B. | AB=ED | C. | CD=AE | D. | EC=AD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
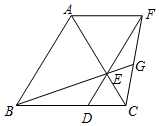 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.
如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
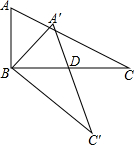 如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( )
如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( )| A. | $\frac{4\sqrt{5}}{5}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com