
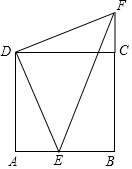
 已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.分析 (1)确定旋转中心及旋转的角度,首先确定哪是对应点,即可确定旋转中心以及旋转角;
(2)根据旋转的性质,可以得到旋转前后的两个图形全等,以及旋转角的定义即可作出判断;
(3)根据△DAE≌△DCF,可以得到:AE=CF,DE=DF,则四边形DEBF的周长就是正方形的三边的和与DE的和.
解答 解:(1)旋转中心是点D.旋转角为90度;
(2)△DFE的形状是等腰直角三角形,
理由:根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形;
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=20;
点评 本题主要考查了旋转的性质,掌握“旋转不改变图形的形状与大小,只改变图形的位置,旋转前后两个图形全等”是解题的关键.


科目:初中数学 来源: 题型:选择题
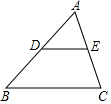 如图,DE∥BC,在下列比例式中,不能成立的是( )
如图,DE∥BC,在下列比例式中,不能成立的是( )| A. | $\frac{AB}{AD}$=$\frac{AC}{AE}$ | B. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | C. | $\frac{AD}{DB}$=$\frac{DE}{BC}$ | D. | $\frac{AD}{DE}$=$\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
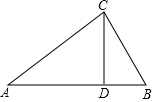 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为1000元/m,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com