【题目】如图，在四边形ABCD中，
，
，
，
，点E在AB边上，
，
．
求CE的长度；
求证：
≌
；
设点P是线段AB上的一个动点，求
的最小值是多少？
心算口算巧算一课一练系列答案
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】某校举行了“文明在我身边”摄影比赛．已知每幅参赛作品成绩记为x分(60≤x＜100)．校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题：
(1)统计表中c的值为________；样本成绩的中位数落在分数段________中；
(2)补全频数直方图；
(3)若80分以上(含80分)的作品将被组织展评，试估计全校被展评的作品数量是多少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1．
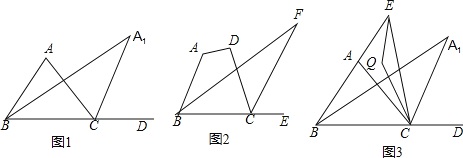
（1）当∠A为70°时，
∵∠ACD －∠ABD=∠____________
∴∠ACD －∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD －∠A1BD=
（∠ACD－∠ABD）
∴∠A1=___________°；
（2）∠A1BC的角平分线与∠A1CD的角平分线交于A2，∠A2BC与A2CD的平分线交于A3，如此继续下去可得A4、…、An，请写出∠A与∠An 的数量关系____________；
（3）如图2，四边形ABCD中，∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角，若∠A+∠D=230度，则∠F= ．
（4）如图3，若E为BA延长线上一动点，连EC，∠AEC与∠ACE的角平分线交于Q，当E滑动时有下面两个结论：①∠Q+∠A1的值为定值；②∠Q —∠A1的值为定值.
其中有且只有一个是正确的，请写出正确的结论，并求出其值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列叙述中，正确的有（ ）
①如果
，那么
；②满足条件
的n不存在；
③任意一个三角形的三条高所在的直线相交于一点，且这点一定在三角形的内部；
④ΔABC中，若∠A+∠B=2∠C, ∠A-∠C=40°，则这个△ABC为钝角三角形．
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CN是等边△
的外角
内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．
（1）依题意补全图形；
（2）若
，求
的大小（用含
的式子表示）；
（3）用等式表示线段
， 
与
之间的数量关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学为了了解七年级学生体能状况，从七年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级，并依据测试成绩绘制了如下两幅尚不完整的统计图：
（1）这次抽样调查的样本容量是 ，并补全条形统计图；
（2）在统计图中B等级所对应的圆心角为 ，D等级学生人数占被调查人数的百分比为 ；
（3）该校七年级学生有1600人，请你估计其中A等级的学生人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
