
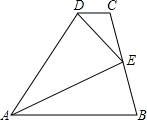
 如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
如图,在四边形ABCD中,AB∥CD,点E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.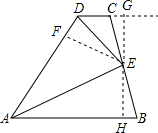 解:过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,
解:过点E作EH⊥AB于点H,反向延长EH交DC的延长线于点G,过点E作EF⊥AD于点F,
|


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
| A、必是甲 | B、必是乙 |
| C、必是丙 | D、不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
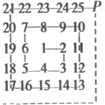 友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )
友谊公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果P处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处(编号2在第1个拐角处)的竹子的编号应为( )| A、10010 |
| B、10101 |
| C、10100 |
| D、10110 |
查看答案和解析>>
科目:初中数学 来源: 题型:
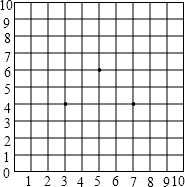 在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.
在图的方格棋盘中放入3枚棋子,位置分别是(3,4),(7,4),(5,6).这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个正方形?如果能,请说出放在什么位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com