
如图①,已知:在矩形ABCD的边AD上有一点O,OA= ,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H
,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H 作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.
作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.
(1)求证:四边形ABHP是菱形;
(2)问△EFG的直角顶点G能落在⊙O上吗?若能,求出此时x的值;若不能,请说明理由;
(3)求S与x之间的函数关系式,并直接写出FG与⊙O相切时,S的值.
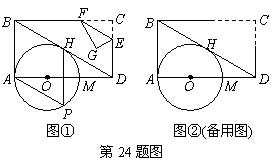
(1)连结OH,如图①.
∵AB∥HP,∠BAD=90°,∴AQ⊥HP.而AM是直径,
∴HQ= HP=
HP=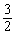 .
.
在Rt△OHQ中,sin∠HOQ=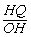 =
=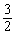 ×
×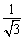 =
=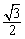 ,
,
∴∠HOQ=60°,则∠OHQ=30°,∠APH=60°.
又BD与⊙O相切,∴∠QHD=90°-∠OHQ=60°.∴∠APH=∠QHD.
∴AP∥BH.
又∵AB∥HP,∴四边形ABHP是平行四边形.
由AB⊥AM,AM是直径知AB是⊙O的切线,而BD也是⊙O的切线,
∴AB=BH.
∴四边形ABHP是菱形.(注:其它方法,请参照给分)
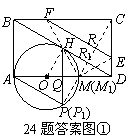

(2)G点能落在⊙O上,如图①.
方法一:过C作射线CR⊥EF交EF于R,交AD于M1,交BD于R1,交AP于P1,则C关于EF对称点G在射线CR上.
当G点落在M1上时,M1E=CE=x,AB=CD=HP=3,AD=AB·tan60°=3 ,ED=CD-CE=3-x.
,ED=CD-CE=3-x.
在Rt△M1DE中,cos60°=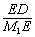 =
=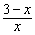 =
= .解得x=2.
.解得x=2.
sin60°=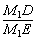 =
=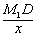 =
=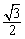 ,∴M1D=
,∴M1D= .
.
而MD=AD-AM= ,∴M1与M重合.
,∴M1与M重合.
∴M在CP1上,则MP1⊥AP,而MP⊥AP,
∴P与P1重合,这校射线CR与⊙O交于M,P.
由AP∥BD,CP⊥AP,CR1=PR1,知C与P关于BD对称.
由于点E不与点D重合,故点G不可能落在P点.
∴点G只能落在⊙O的M点上,此时x=2.
方法二:连结CM,PM,如图①,由(1)知∠AMP=∠APH=60°,tan∠CMD=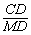 =
= =
= .∴∠CMD=∠AMP=60°.
.∴∠CMD=∠AMP=60°.
∴C,M,P三点共线.
∵∠BDA=30°,∴CM⊥BD.而BD∥EF,
∴CM⊥EF,点C关于EF的对称点G落在CP上.
又∵点P到BD的距离等于点C到BD的距离(即点A到BD的距离),EF与BD不重合,∴点G不能落在P点,可以落在⊙O上的M点.
当点G落在⊙O上的M点时,ME=CE=x,
在Rt△MDE中,x=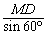 =
= ×
× =2.
=2.
∴点G落在床⊙O上的M点,此时x=2.
方法三:证法略.
提示:过C作C′P⊥AP于P′,交BD于R′,可求CP′=2CR′=3 ,PM+CM=3
,PM+CM=3 ,则CP′=CM+MP,从而C,M,P三点共线,x的值求法同上.
,则CP′=CM+MP,从而C,M,P三点共线,x的值求法同上.
(3)由(2)知:①当点G在CM上运动时,0<x≤2,
S= x·
x· x=
x=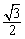 x2.
x2.
②当点G在PM上运动时,2<x<3,设FG交AD于T,EG交AD于N,如图②,


则:EG=CE=x,ED=3-x,S△EFG= CE·CF=
CE·CF=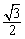 x2.
x2.
NE=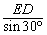 =6-2x,GN=GE-NE=3x-6.
=6-2x,GN=GE-NE=3x-6.
∵TG=GN·tan30°=(3x-6)×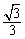 =
= x-2
x-2 .
.
S=S△EFG-S△TGN=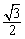 x2-
x2-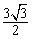 x2+6
x2+6 x-6
x-6
=- x2+6
x2+6 x-6
x-6 .
.
综上所述,S=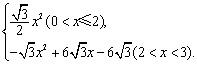
当FG与⊙O相切时,S=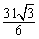 -6.
-6.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
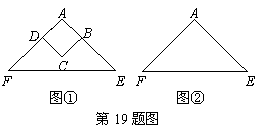
如图①,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度α(0°<α<90°)后,连结BE,DF.请在图②中用实线补全图形,这时DF=BE还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )
|
| A. | 1 | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源: 题型:
张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是,矩形的周长是2(x+);当矩形成为正方形时,就有x=(0>0),解得x=1,这时矩形的周长2(x+)=4最小,因此x+(x>0)的最小值是2.模仿张华的推导,你求得式子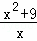 (x>0)的最小值是( )
(x>0)的最小值是( )
|
| A. | 2 | B. | 1 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线。能解释这一实际应用的数学知识是
A. 两点确定一条直线 B. 两点之间线段最短
C. 垂线段最短 D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com