
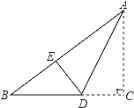
【题目】如图,一张纸片的形状为直角三角形,其中∠C=90°,AC=12cm,BC=16cm,沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,则CD的长为______cm.
【答案】6;
【解析】
在Rt△ABC中根据勾股定理得AB=20,再根据折叠的性质得AE=AC=12,DE=DC,∠AED=∠C=90°,所以BE=AB-AE=8,设CD=x,则BD=16-x,然后在Rt△BDE中利用勾股定理得到82+x2=(16-x)2,再解方程求出x即可.
在Rt△ABC中,∵AC=12,BC=16,
∴AB=![]() =20,
=20,
∵△ACB沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,
∴AE=AC=12,DE=DC,∠AED=∠C=90,
∴BE=ABAE=2012=8,
设CD=x,则BD=16x,
在Rt△BDE中,∵BE2+DE2=BD2,
∴82+x2=(16x)2,解得x=6,
即CD的长为6cm.
故答案为6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两位采购员同时去一家饲料公司买两次饲料,两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料,购买的饲料单价分别为m元/千克和n元/千克,
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
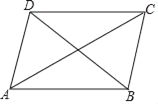
【题目】如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( )
A. α B. ![]() C. 90﹣α D. 90﹣
C. 90﹣α D. 90﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16)
(2)![]()
(3)﹣22÷(﹣4)3+|0.8﹣1|×(2![]() )2
)2
(4)4xy+(3y2﹣2x2)﹣(5xy﹣2x2)﹣4y2
(5)先化简,再求值:![]() x﹣2(x﹣y2)+(﹣
x﹣2(x﹣y2)+(﹣![]() x+
x+![]() y2),其中x=﹣
y2),其中x=﹣![]() ,y=3
,y=3
查看答案和解析>>
科目:初中数学 来源: 题型:
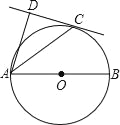
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若CD=4,AD=8,试求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
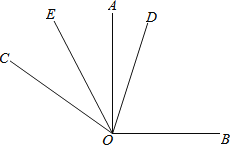
【题目】如图,已知同一平面内∠AOB=90°,∠AOC=60°.
(1)问题发现:∠BOD的余角是 ,∠BOC的度数是 ;
(2)拓展探究:若OD平分∠BOC,OE平分∠AOC,则∠DOE的度数是 ;
(3)类比延伸:在(2)条件下,如果将题目中的∠AOB=90°改为∠AOB=2∠β;∠AOC=60°改为∠AOC=2α(α<45°),其他条件不变,你能求出∠DOE吗?若能,请你写出求解过程:若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
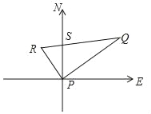
【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
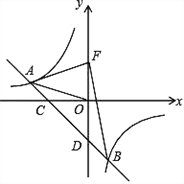
【题目】如图,一次函数 yax 2(a0) 的图象与反比例函数 y![]() (k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=
(k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=![]() ,AO=
,AO=![]() .
.
(1)求这个一次函数和反比例函数的解析式;
(2) 若点 F 是点D 关于 x 轴的对称点,求△ABF 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com