
【题目】如图,分别以Rt△ABC的直角边AC、BC为边,在Rt△ABC外作两个等边三角形△ACE和△BCF,连接BE、AF分别交AC、BC边于H、D两点.下列结论:①AF=BE;②∠AFC=∠EBC;③∠FAE=90°;④BD=FD,其中正确结论的个数是( )

A.4个B.3个C.2个D.1个
【答案】C
【解析】
由等边三角形的性质得出BC=CF,CE=AC,∠BCF=∠ACE=∠CFB=∠CBF=∠CAE=60°,∠ACB=90°,易证∠BCE=∠FCA=150°,由SAS证得△BCE≌△FCA,得出AF=BE,∠AFC=∠EBC,由∠FCA=150°,得出∠FAC<30°,则∠FAE=∠FAC+∠CAE<90°,由∠BFD<∠BFC,得出∠BFD<∠CBF,则DF>BD,即可得出结果.
∵△ACE和△BCF是等边三角形,
∴BC=CF,CE=AC,∠BCF=∠ACE=∠CFB=∠CBF=∠CAE=60°,∠ACB=90°,
∴∠BCE=90°+60°=150°,∠FCA=60°+90°=150°,
∴∠BCE=∠FCA.
在△BCE和△FCA中,∵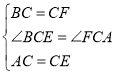 ,
,
∴△BCE≌△FCA(SAS),
∴AF=BE,∠AFC=∠EBC,故①、②正确;
∵∠FCA=60°+90°=150°,∴∠FAC<30°.
∵∠CAE=60°,∴∠FAE=∠FAC+∠CAE<90°,故③错误;
∵∠BFD<∠BFC,∴∠BFD<∠CBF,∴DF>BD,故④错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
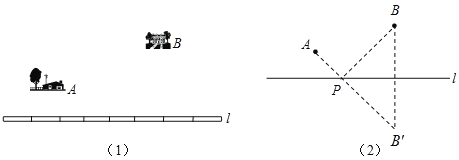
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
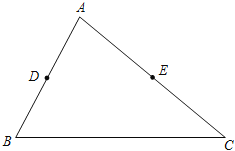
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题:
①方程![]() 的解为
的解为 ![]() ;
;
②方程![]() 的解为
的解为 ![]() ,
,![]() ;
;
③方程![]() 的解为
的解为 ![]() ,
,![]() ;
;
…
(1)根据以上方程特征及其解的特征,请猜想:
①方程![]() 的解为________;
的解为________;
②关于![]() 的方程________的解为
的方程________的解为![]() ,
,![]() .
.
(2)请用配方法解方程![]() ,以验证猜想结论的正确性.
,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
用时的频数 用时 线路 |
|
|
| 合计 |
3路 | 260 | 167 | 23 | 450 |
121路 | 160 | 166 | 124 | 450 |
26路 | 50 | 122 | 278 | 450 |
早高峰期间,乘坐__________(“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 分别为
分别为![]() 的直径和弦,
的直径和弦,![]() 为
为![]() 的中点,
的中点,![]() 垂直于
垂直于![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,下列结论一定错误的是( )
,下列结论一定错误的是( )

A. DE是⊙O的切线 B. 直径AB长为20cm
C. 弦AC长为16cm D. C为![]() 的中点
的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(2﹣a)x﹣2(a>0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.给出下列结论:
①在a>0的条件下,无论a取何值,点A是一个定点;
②在a>0的条件下,无论a取何值,抛物线的对称轴一定位于y轴的左侧;
③y的最小值不大于﹣2;
④若AB=AC,则a=![]() .
.
其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com