
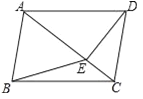
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
【答案】(1)证明见解析;(2)BE⊥AC;(3)![]() .
.
【解析】
试题分析:(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;
(2)求出AD=DC,根据菱形的判定得出四边形ABCD是菱形,根据等腰三角形的性质得出即可;
(3)根据等边三角形的性质得出AB=AE,∠BAC=60°,求出∠DCE=∠BAE=60°,求出CD=2EC,设CE=x,则AB=DC=AE=2x,根据勾股定理得出方程,求出x,即可得出答案.
试题解析:(1)证明:∵AB∥CD,∴∠ABC+∠DCB=180°,∵∠ABC=∠ADC,∴∠ADC+∠BCD=180°,∴AD∥BC,∵AB∥CD,∴四边形ABCD是平行四边形;
(2)解:BE⊥AC,理由是:∵DE⊥AC,E为AC的中点,∴AD=DC,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形,∴AB=BC,∵E为AC的中点,∴BE⊥AC;
(3)解:∵△ABE是等边三角形,∴AB=AE,∠BAC=60°,∵AB∥DC,∴∠DCE=∠BAE=60°,∵∠DEC=90°,∴∠CDE=30°,∴CD=2EC,设CE=x,则AB=DC=AE=2x,由勾股定理得:DE2=AD2﹣AE2=DC2﹣CE2,即![]() ,解得:x=
,解得:x=![]() (负数舍去),即CE=
(负数舍去),即CE=![]() ,AE=
,AE=![]() ,∴AC=
,∴AC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?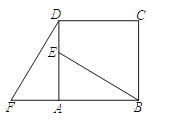
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( ) 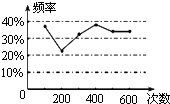
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com