
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( ) .
A.AC⊥BDB.四边形ABCD是菱形
C.AC=BCD.△ABO≌△CDO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买12台节能新设备,现有甲乙两种型号的设备可供选购,经调查,购4台甲比购3台乙多用18万元,购3台甲比购4台乙少用4万元。
(1)求甲乙两种设备的单价。
(2)该公司决定购买甲设备不少于5台,购买资金不超过136万元,你认为该公司有几种购买方案?并直接写出最省钱的购买方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
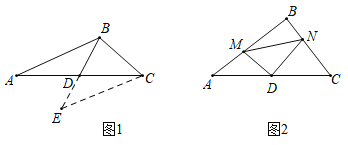
【题目】(1)阅读理解:如图1,在![]() 中,若
中,若![]() ,
,![]() .求
.求![]() 边上的中线
边上的中线![]() 的取值范围.小聪同学是这样思考的:延长
的取值范围.小聪同学是这样思考的:延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() .利用全等将边
.利用全等将边![]() 转化到
转化到![]() ,在
,在![]() 中利用三角形三边关系即可求出中线
中利用三角形三边关系即可求出中线![]() 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线
的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线![]() 的取值范围是__________.
的取值范围是__________.
(2)问题解决:如图2,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,若
边上,若![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接CE、DE、AC,CE与AD交于点F.

(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B.求证:四边形ACDE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为: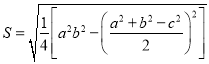 ①(其中
①(其中![]() 为三角形的三边长,
为三角形的三边长,![]() 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;![]() ……②(其中
……②(其中![]() )
)
材料二:对于平方差公式:![]() 公式逆用可得:
公式逆用可得:![]() ,例:
,例:![]()
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,且BA=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
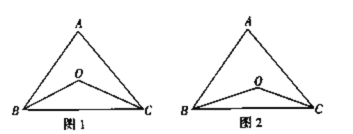
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com