
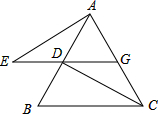
 已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.
已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.分析 (1)根据已知等边三角形的性质可推出△ADG是等边三角形,从而再利用SAS判定△AGE≌△DAC;
(2)连接AF,由已知可得四边形EFCD是平行四边形,从而得到EF=CD,∠DEF=∠DCF,由(1)知△AGE≌△DAC得到AE=CD,∠AED=∠ACD,从而可得到EF=AE,∠AEF=60°,所以△AEF为等边三角形.
解答 证明:(1)在△AGE与△DAC中,
∵DG‖BC,△ABC是等边三角形
∴AD=AG=DG
又∵DE=CG
∴EG=DE+DG=CG+AG=AC,
∠AGE=∠DAC=60°
在△AGE和△DAC中,
$\left\{\begin{array}{l}{AG=AD}\\{∠AGE=∠DAC}\\{GE=AC}\end{array}\right.$,
∴△AGE≌△DAC
(2)判断:△AEF是等边三角形
证明:∵EF∥DC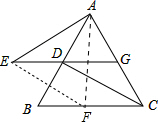
∴∠GEF=∠GDC
又∵∠AEG=∠ACD
∴∠AEG+∠GEF=∠GCD+∠GDC=∠AGD=60°
∴∠AEF=60°
又∵DG∥BC,EF∥DC
∴四边形CDEF是平行四边形
∴DC=EF
又∵△AGE≌△DAC
∴AE=DC
∴AE=EF
∴△AEF是等边三角形.
点评 此题主要考查学生对全等三角形的判定,等边三角形的性质及判定的理解及运用.


科目:初中数学 来源: 题型:填空题
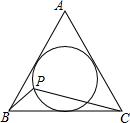 点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.
点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
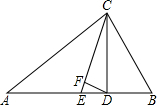 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
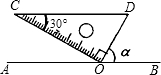 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形ABCD边BC的中点F,交CD于点E,四边形AFCE的面积为2,则k的值为2.
已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形ABCD边BC的中点F,交CD于点E,四边形AFCE的面积为2,则k的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
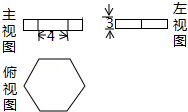 如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )| A. | 24$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | 72$\sqrt{3}$ | D. | 144$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com