
 如图,正方形ABCD中,AB=30,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G.连接AG、CF.下列结论:①△ABG≌△AFG;②BG=15;③△CFG是正三角形;④△FGC的面积为90.其中正确的是①②④(填所有正确答案的序号).
如图,正方形ABCD中,AB=30,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G.连接AG、CF.下列结论:①△ABG≌△AFG;②BG=15;③△CFG是正三角形;④△FGC的面积为90.其中正确的是①②④(填所有正确答案的序号). 分析 ①根据折叠的性质可以得到∠B=∠AFG=90°,AB=AF,AG=AG,根据HL定理即可证明两三角形全等;
②不妨设BG=FG=x,(x>0),则CG=30-x,EG=10+x,在Rt△CEG中,利用勾股定理即可列方程求得;
③利用②得出的结果,结合折叠的性质求得答案即可;
④根据三角形的面积公式可得:S△FGC=$\frac{3}{5}$S△EGC,即可求解.
解答 解:①在正方形ABCD中,AD=AB,∠D=∠B=∠C=90°,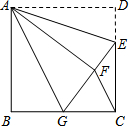
又∵△ADE沿AE对折至△AFE,延长EF交边BC于点G
∴∠AFG=∠AFE=∠D=90°,AF=AD,
即有∠B=∠AFG=90°,AB=AF,AG=AG,
在直角△ABG和直角△AFG中,
$\left\{\begin{array}{l}{AB=AF}\\{AG=AG}\end{array}\right.$,
∴△ABG≌△AFG;正确.
②∵AB=6,点E在边CD上,且CD=3DE,
∴DE=FE=10,CE=20,
不妨设BG=FG=x,(x>0),
则CG=30-x,EG=10+x,
在Rt△CEG中,(10+x)2=202+(30-x)2
解得x=15,于是BG=GC=15;正确.
③∵BG=GF=CG,
∴△CFG是等腰三角形,
∵BG=$\frac{1}{2}$AB,
∴∠AGB≠60°,
则∠FGC≠60°,
∴△CFG不是正三角形.错误.
④∵$\frac{GF}{FE}$=$\frac{3}{2}$,
∴$\frac{GF}{GE}$=$\frac{3}{5}$,
∴S△FGC=$\frac{3}{5}$S△EGC=$\frac{3}{5}$×$\frac{1}{2}$×20×15=90.正确.
正确的结论有①②④.
故答案为:①②④.
点评 本题考查了正方形的性质,以及图形的折叠的性质,三角形全等的证明,理解折叠的性质是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
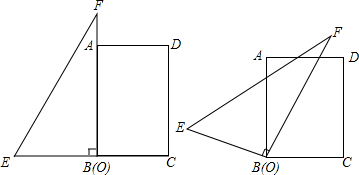
 如图,已知A是定角∠MON的平分线上的一个定点,过A任作一条直线与OM、ON分别交于P、Q,求证:$\frac{1}{OP}$+$\frac{1}{OQ}$为定值.
如图,已知A是定角∠MON的平分线上的一个定点,过A任作一条直线与OM、ON分别交于P、Q,求证:$\frac{1}{OP}$+$\frac{1}{OQ}$为定值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
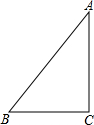 如图是一个直角三角形纸片,其中∠C=90°,两直角边长分别为3cm,4cm,现要给这个纸片再拼接一个直角三角形纸片,两纸片不重叠且无缝隙,使得拼接后的纸片形状是等腰三角形,拼接成的等腰三角形的纸片的周长为16或18cm.
如图是一个直角三角形纸片,其中∠C=90°,两直角边长分别为3cm,4cm,现要给这个纸片再拼接一个直角三角形纸片,两纸片不重叠且无缝隙,使得拼接后的纸片形状是等腰三角形,拼接成的等腰三角形的纸片的周长为16或18cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com