
在平面直角坐标系xOy中,二次函数 的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).
的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).
(1)求m的值及点A的坐标;
(2)如图,将△AEO沿x轴向右平移得到△A′E′O′,连结A′B、BE′.
①当点E′落在该二次函数的图象上时,求AA′的长;
②设AA′=n,其中0<n<2,试用含n的式子表示A′B2+BE′2,并求出使 A′B2+BE′2取得最小值时点E′的坐标;
A′B2+BE′2取得最小值时点E′的坐标;
③当A′B+BE′取得最小值时,求点E′的坐标.
 |
解:(1)由题意可知  ,
, .
.
∴ 二次函数的解析式为 .
.
∴ 点A的坐标为(- 2, 0)
(2)①∵ 点E(0,1),由题意可知,
 .
.
解得  .
.
∴ AA′= .
.
 ②如图,连接EE′.
②如图,连接EE′.
由题设知AA′=n(0<n<2),则A′O = 2 - n.
在Rt△A′BO中,由A′B2 = A′O2 + BO2,
得A′B2 =(2–n)2 + 42 = n2 - 4n + 20.
∵△A′E′O′是△AEO沿x轴向右平移得到的,
∴EE′∥AA′,且EE′=AA′.
∴∠BEE′=90°,EE′=n.
又BE=OB - OE=3.
∴在Rt△BE′E中,BE′2 = E′E2 + BE2 = n2 + 9,
∴A′B2 + BE′2 = 2n2 - 4n + 29 = 2(n–1)2 + 27.
当n = 1时,A′B2 + BE′2可以取得最小值,此时点E′的坐标是(1,1).
③如图,过点A作AB′⊥x轴,并使AB′ = BE = 3.
易证△AB′A′≌△EBE′,
∴B′A′ = BE′,
∴A′B + BE′ = A′B + B′A′.
当点B,A′,B′在同一条直线上时,A′B + B′A′最小,即此时A′B+BE′取得最小值.
易证△AB′A′∽△OBA′,
∴ ,
,
∴AA′= ,
,
∴EE′=AA′= ,
,
∴点E′的坐标是( ,1
,1 ).
).


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
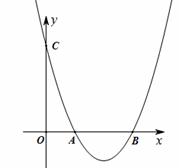
如图 , 已知二次函数y = x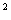 -4x + 3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
-4x + 3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
 解:
解:
查看答案和解析>>
科目:初中数学 来源: 题型:
在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
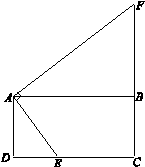
如图,在矩形ABCD中,E是CD边上任意一点(不与点C,D重合),作AF⊥AE交CB的延长线于点F.
(1)求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2,设DE=x,
①求点M到FC的距离(用含x的代数式表示);
②连接BM,设 ,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com