
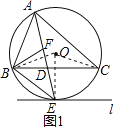
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
【答案】
(1)
直线l与⊙O相切.
理由:如图1所示:连接OE、OB、OC.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴ ![]() .
.
∴∠BOE=∠COE.
又∵OB=OC,
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切
(2)
解:∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)
由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴ ![]() ,即
,即 ![]() ,解得;AE=
,解得;AE= ![]() .
.
∴AF=AE﹣EF= ![]() ﹣7=
﹣7= ![]()
【解析】(1)连接OE、OB、OC.由题意可证明 ![]() ,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.本题主要考查的是圆的性质、相似三角形的性质和判定、等腰三角形的性质、三角形外角的性质、切线的判定,证得∠EBF=∠EFB是解题的关键.
,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.本题主要考查的是圆的性质、相似三角形的性质和判定、等腰三角形的性质、三角形外角的性质、切线的判定,证得∠EBF=∠EFB是解题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,
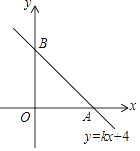
(1)求这条直线的解析式;
(2)若将这条直线沿x轴翻折,求翻折后得到的直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.

(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
(2)用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数;
(3)求第n行各数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数![]() 的图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是________.
的图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是________.
【答案】![]()
【解析】试题分析:∵函数y=![]() 中,k=-1<0,
中,k=-1<0,
∴此函数的图象的两个分支位于二四象限,且在每一象限内,y随x的增大而增大.
∵x1<0<x2<x3,
∴点A(x1,y1)在第二象限,B(x2,y2)、C(x3,y3)在第四象限,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
故答案为:y2<y3<y1.
点睛:本题考查的是反比例函数图象的性质,当k>0时,图象位于一三象限,在每一个象限内y随x的增大而减小,k<0时,图象位于二四象限,在每一个象限内,y随x的增大而增大.
【题型】填空题
【结束】
14
【题目】如图,直线y=kx(k<0)与双曲线![]() 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°
(1)求发射台与雷达站之间的距离LR;
(2)求这枚火箭从A到B的平均速度是多少(结果精确到0.01)?
(参考数据:son42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
【答案】(1) ![]() ;(2)x=
;(2)x=![]()
【解析】试题分析:(1)两边乘以(x-1)(2x+1)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可;
(2)两边乘以(x+2)(x-2)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可.
试题解析:
解:(1)两边乘以(x-1)(2x+1)去分母得:2x+1=5(x-1),
解得:x=2,
当x=2时,(x-1)(2x+1)≠0,
∴原分式方程的解为x=2;
(2)两边乘以(x+2)(x-2)去分母得:(x-2)2-3=(x+2)(x-2),
解得:x=![]() ,
,
当x=![]() 时,(x+2)(x-2)≠0,
时,(x+2)(x-2)≠0,
所以原分式方程的解为x=![]() .
.
【题型】解答题
【结束】
21
【题目】先化简,再求值![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取.
的整数解中选取.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
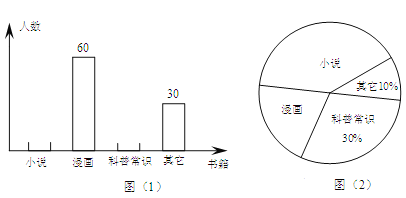
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com