练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，某电信公司提供了A，B两种方案的移动通讯费用y（元）与通话时间x（元）之间的关系，则下列结论中正确的有（　　）

    (1)若通话时间少于120分，则A方案比B方案便宜20元；

    (2)若通话时间超过200分，则B方案比A方案便宜12元；

    (3)若通讯费用为60元，则B方案比A方案的通话时间多；

    (4)若两种方案通讯费用相差10元，则通话时间是145分或185分．

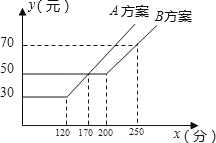
    A. 1个 B. 2个 C. 3个 D. 4个

    【答案】C

    【解析】

    试题当B方案为50元时，A方案如果是40元或者60元，才能使两种方案通讯费用相差10元，先求两种方案的函数解析式，再求对应的时间．

    试题解析：A方案的函数解析式为：yA=；

    B方案的函数解析式为：yB=；

    当B方案为50元，A方案是40元或者60元时，两种方案通讯费用相差10元，

    将yA=40或60代入，得x=145分或195分，故D错误；

    观察函数图象可知（1）、（2）、（3）正确．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点D是△ABC内一点，点E，F，G，H分别是AB，AC，CD，BD的中点。

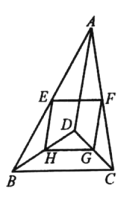
    （1）求证：四边形EFGH是平行四边形；（2）已知AD＝6，BD＝4，CD＝3，∠BDC＝90°，求四边形EFGH的周长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】梧桐山是深圳最高的山峰，某校综合实践活动小组要测量“主山峰”的高度，先在梧桐山对面广场的A处测得“峰顶”C的仰角为45°，此时，他们刚好与峰底D在同一水平线上.然后沿着坡度为30°的斜坡正对着“主山峰”前行700米，到达B处，再测得“峰顶”C的仰角为60°，如图，根据以上条件求出“主山峰”的高度？(测角仪的高度忽略不计，结果精确到1米).参考数据：（1.4，1.7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

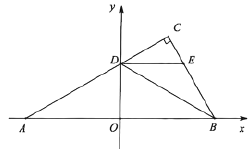
    【题目】如图平面直角坐标系中，点，在轴上，，点在轴上方，，，线段交轴于点，，连接，平分，过点作交于．

    （1）点的坐标为 ．

    （2）将沿线段向右平移得，当点与重合时停止运动，记与的重叠部分面积为，点为线段上一动点，当时，求的最小值；

    （3）当移动到点与重合时，将绕点旋转一周，旋转过程中，直线分别与直线、直线交于点、点，作点关于直线的对称点，连接、、．当为直角三角形时，直接写出线段的长．

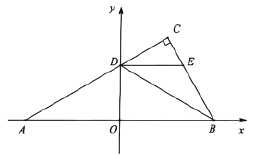
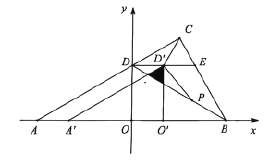
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市今年中考理化实验操作考试，采用学生抽签方式决定自己的考试内容．规定每位考生必须在三个物理实验（用纸签A、B、C表示）和三个化学试验（用纸签D、E、F表示）中各抽取一个实验操作进行考试，小刚在看不到纸签的情况下，分别从中各随机抽取一个．用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

    （1）证明与推断：

    ①求证：四边形CEGF是正方形；

    ②推断：的值为　 　：

    （2）探究与证明：

    将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

    （3）拓展与运用：

    正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知矩形ABCD，把△BCD沿BD翻折，得△BDG，BG，AD所在的直线交于点E，过点D作DF∥BE交BC所在直线于点F．

    （1）求证：四边形DEBF是菱形；

    （2）若AB＝8，AD＝4，求四边形BEDF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

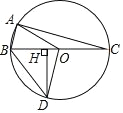
    【题目】如图，⊙O 是△ABC 的外接圆，BC 是直径，AC＝2DH，过点 D 作 DH 垂直BC 于点 H，以下结论中：①BH＝HD；②∠BAO＝∠BOD；③；④连接 AO、BD，若 BC＝8，sin∠HDO＝ ，则四边形 ABDO 的面积为， 其中正确的结论是 ____（请填写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

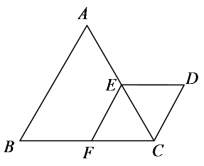
    【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB．

    （1）求证：四边形EFCD是菱形；

    （2）设CD＝2，求D、F两点间的距离．

    查看答案和解析>>

    同步练习册答案