
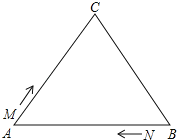
【题目】如图,![]() 中,
中,![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,
分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,![]() 、
、![]() 同时停止运动.
同时停止运动.
(1)点![]() 、
、![]() 运动几秒时,
运动几秒时,![]() 、
、![]() 两点重合?
两点重合?
(2)点![]() 、
、![]() 运动几秒时,可得到等边三角形
运动几秒时,可得到等边三角形![]() ?
?
(3)当点![]() 、
、![]() 在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时
在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时![]() 、
、![]() 运动的时间.
运动的时间.
【答案】(1)12;(2)4;(3)能,此时M、N运动的时间为16秒.
【解析】
(1)首先设点M、N运动x秒后,M、N两点重合,表示出M,N的运动路程,N的运动路程比M的运动路程多12cm,列出方程求解即可;
(2)根据题意设点M、N运动t秒后,可得到等边三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=AN,三角形ANM就是等边三角形;
(3)首先假设△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,列出方程,可解出未知数的值.
(1)设点M、N运动x秒时,M、N两点重合,
x×1+12=2x,
解得:x=12;
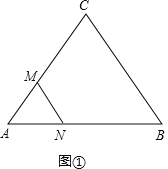
(2)设点M、N运动t秒时,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=12﹣2t.
∵三角形△AMN是等边三角形,∴t=12﹣2t,
解得:t=4,∴点M、N运动4秒时,可得到等边三角形△AMN.
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,∴∠AMC=∠ANB.
∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,
在△ACM和△ABN中,
∵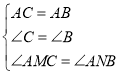 ,∴△ACM≌△ABN,∴CM=BN,
,∴△ACM≌△ABN,∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,∴CM=y﹣12,NB=36﹣2y,CM=NB,
y﹣12=36﹣2y,
解得:y=16.故假设成立,∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.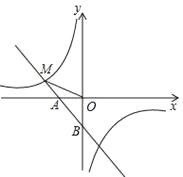
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人赛跑,两人所跑的路程![]() (米)与所用时间
(米)与所用时间![]() (分)的函数关系如图所示,给出下列结论:①比赛全程1500米;②2分时,甲乙相距300米;③比赛结果是乙比甲领先30秒到达终点;④3分40秒时乙追上甲,其中正确结论的个数为( )
(分)的函数关系如图所示,给出下列结论:①比赛全程1500米;②2分时,甲乙相距300米;③比赛结果是乙比甲领先30秒到达终点;④3分40秒时乙追上甲,其中正确结论的个数为( )
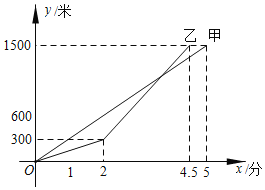
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某商场有可上行和下行的两条自动扶梯,扶梯上行和下行的长度相等,运行速度相同且保持不变,甲、乙两人同时站上了上行和下行端,甲站上上行扶梯的同时又以0.8米/秒的速度往上走,乙站上下行扶梯后则站立不动随扶梯下行,甲到达扶梯顶端后立即乘坐下行扶梯(换乘时间忽略不计)同时以0.8米/秒的速度往下走,乙到达低端后则在原点等候甲,图②中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中,高扶梯底端的路程y(米)与所用时间x(秒)的部分函数图象,结合图象解答下列问题:
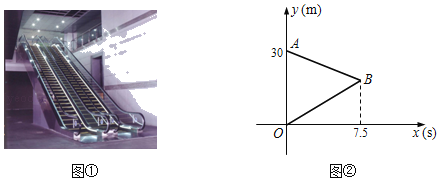
(1)每条扶梯的长度为 米(直接填空);
(2)求点B的坐标;
(3)乙到达扶梯底端后,还需等待 秒,甲才到达扶梯底端(直接填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔![]() 前的平地上选择一点
前的平地上选择一点![]() ,树立测角仪
,树立测角仪![]() ,测出看塔顶的仰角约为
,测出看塔顶的仰角约为![]() ,从
,从![]() 点向塔底
点向塔底![]() 走
走![]() 米到达
米到达![]() 点,测出看塔顶的仰角约为
点,测出看塔顶的仰角约为![]() ,已知测角仪器高为
,已知测角仪器高为![]() 米,则塔
米,则塔![]() 的高大约为
的高大约为![]() ( )
( )
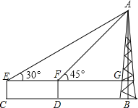
A. 141米 B. 101米 C. 91米 D. 96米
查看答案和解析>>
科目:初中数学 来源: 题型:
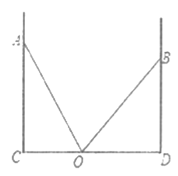
【题目】如图,已知![]() 、
、![]() 为数值的墙面(
为数值的墙面(![]() ),一架梯子从点
),一架梯子从点![]() 竖起当靠在墙面
竖起当靠在墙面![]() 上时,梯子的另一端落在点
上时,梯子的另一端落在点![]() 处,此时
处,此时![]() ,当靠在墙面
,当靠在墙面![]() 上时,梯子的另一端落在点
上时,梯子的另一端落在点![]() 处,此时
处,此时![]() ,且
,且![]() 米.
米.
(1)求梯子的长;
(2)求![]() 、
、![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com