
【题目】如图1,对于平面上不大于![]() 的
的![]() ,我们给出如下定义:若点P在
,我们给出如下定义:若点P在![]() 的内部或边界上,作
的内部或边界上,作![]() 于点E,.
于点E,.![]() 于点
于点![]() ,则称
,则称![]() 为点P相对于
为点P相对于![]() 的“优点距离”,记为
的“优点距离”,记为![]()

如图2,在平面直角坐标系xOy中,对于![]() ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足![]() 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.
(1)满足条件的其中一个点P的坐标是 __,图形G与坐标轴围成图形的面积等于 __ ;
(2)设图形G与x轴的公共点为点A,如图3,已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如果抛物线![]() 经过(2)中的A,B两点,点Q在A,B两点之间的物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的物线上(点Q可与A,B两点重合),求当![]() 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.
【答案】(1)满足条件的其中一个点P的坐标是(5,0);(说明:点P(x,y)的坐标满足x+y=5, 0≤x≤5,0≤y≤5均可),图形G与坐标轴围成图形的面积等于![]() .
.
(2)d(M,∠AOB)=![]() ;
;
(3)点Q的坐标为(4,![]() ).
).
【解析】
试题(1)点P(x,y)的坐标满足x+y=5, 0≤x≤5,0≤y≤5均可, 图形G与坐标轴围成图形的面积等于![]() ;
;
(2)作ME⊥OB于点E,MF⊥x轴于点F,则MF =1,作MD∥x轴,交OB于点D,作BK⊥x轴于点K.
由点B的坐标为B(3,4),可求得直线OB对应的函数关系式为y=![]() x.从而确定 点D的坐标为D(
x.从而确定 点D的坐标为D(![]() ,1),DM=4-
,1),DM=4-![]() =
=![]() .从而可得 OB=5,sin∠AOB=
.从而可得 OB=5,sin∠AOB=![]() ,sin∠MDE=sin∠AOB=
,sin∠MDE=sin∠AOB=![]() ,继而得ME=DM·sin∠MDE=
,继而得ME=DM·sin∠MDE=![]() ,从而得d(M,∠AOB)=
,从而得d(M,∠AOB)=![]() ;
;
(3)由待定系数法得抛物线对应的函数关系式为y=-![]() x2+2x+
x2+2x+![]() ;作QG⊥OB于点G,QH⊥x轴于点H.作QN∥x轴,交OB于点N.设点Q的坐标为Q(m,n),其中3≤m≤5,则QH=n=-
;作QG⊥OB于点G,QH⊥x轴于点H.作QN∥x轴,交OB于点N.设点Q的坐标为Q(m,n),其中3≤m≤5,则QH=n=-![]() m2+2m+
m2+2m+![]() ;同(2)得 sin∠QNG=sin∠AOB=
;同(2)得 sin∠QNG=sin∠AOB=![]() ,从而得点N的坐标为N(
,从而得点N的坐标为N(![]() n,n),NQ=m-
n,n),NQ=m-![]() n.继而得 QG=
n.继而得 QG=![]() m-
m-![]() n,从而得d(Q,∠AOB)=-
n,从而得d(Q,∠AOB)=-![]() (m-4)2+
(m-4)2+![]() , 进而得 当m=4(在3≤m≤5范围内)时,d(Q,∠AOB)取得最大值(
, 进而得 当m=4(在3≤m≤5范围内)时,d(Q,∠AOB)取得最大值(![]() ).
).
此时点Q的坐标为(4,![]() ).
).
试题解析:(1)满足条件的其中一个点P的坐标是(5,0);(说明:点P(x,y)的坐标满足x+y=5, 0≤x≤5,0≤y≤5均可)
图形G与坐标轴围成图形的面积等于![]() .
.
如答图1,作ME⊥OB于点E,MF⊥x轴于点F,则MF =1,作MD∥x轴,交OB于点D,作BK⊥x轴于点K.
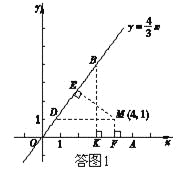
由点B的坐标为B(3,4),可求得直线OB对应的函数关系式为y=![]() x.∴ 点D的坐标为D(
x.∴ 点D的坐标为D(![]() ,1),DM=4-
,1),DM=4-![]() =
=![]() .
.
∴ OB=5,sin∠AOB=![]() ,sin∠MDE=sin∠AOB=
,sin∠MDE=sin∠AOB=![]() ,∴ME=DM·sin∠MDE=
,∴ME=DM·sin∠MDE=![]() ×
×![]() =
=![]() ,∴d(M,∠AOB)=ME+MF=
,∴d(M,∠AOB)=ME+MF=![]() +1=
+1=![]() ;
;
(3)∵ 抛物线y=-![]() x2+bx+c经过A(5,0),B(3,4)两点,
x2+bx+c经过A(5,0),B(3,4)两点,
∴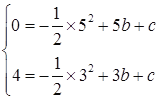 ,解得
,解得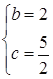 ,∴ 抛物线对应的函数关系式为y=-
,∴ 抛物线对应的函数关系式为y=-![]() x2+2x+
x2+2x+![]() ;
;
如答图2,作QG⊥OB于点G,QH⊥x轴于点H.作QN∥x轴,交OB于点N.

设点Q的坐标为Q(m,n),其中3≤m≤5,则QH=n=-![]() m2+2m+
m2+2m+![]() ;同(2)得 sin∠QNG=sin∠AOB=
;同(2)得 sin∠QNG=sin∠AOB=![]() .
.
∴ 点N的坐标为N(![]() n,n),NQ=m-
n,n),NQ=m-![]() n.∴ QG=NQ·sin∠QNG=
n.∴ QG=NQ·sin∠QNG=![]() (m-
(m-![]() n)=
n)=![]() m-
m-![]() n.
n.
∴d(Q,∠AOB)=QG+QH=![]() m-
m-![]() n+n=
n+n=![]() m+
m+![]() n=
n=![]() m+
m+![]() (-
(-![]() m2+2m+
m2+2m+![]() )=-
)=-![]() (m-4)2+
(m-4)2+![]() ,
,
∴ 当m=4(在3≤m≤5范围内)时,d(Q,∠AOB)取得最大值![]() .
.
此时点Q的坐标为(4,![]() ).
).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
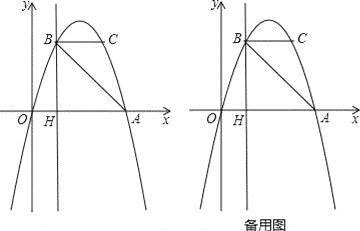
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 | 成活数 | 成活率 | 移植棵数 | 成活数 | 成活率 |
50 | 47 |
| 1500 | 1335 |
|
270 | 235 |
| 3500 | 3203 |
|
400 | 369 |
| 7000 | 6335 |
|
750 | 662 |
| 14000 | 12628 |
|
下面有四个推断:
①当移植的树数是1500时,表格记录成活数是1335,所以这种树苗成活的概率是![]() ;
;
②随着移植棵数的增加,树苗成活的频率总在![]() 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是
附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是![]() ;
;
③若小张移植10000棵这种树苗,则可能成活9000棵;
④若小张移植20000棵这种树苗,则一定成活18000棵.
其中合理的是![]()
![]()
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
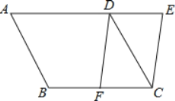
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.
如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.
若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……
△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是__,点A2018的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
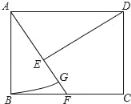
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com