
 已知:四边形ABCD的面积为8068,边BA与CD的延长线交于E点,点F、G分别是四边形对角线的中点.求△EFG的面积.
已知:四边形ABCD的面积为8068,边BA与CD的延长线交于E点,点F、G分别是四边形对角线的中点.求△EFG的面积. 分析 利用三角形的一条中线将三角形分成面积相等的两个三角形,以及面积的和与差得出S△EFG=$\frac{1}{4}$S四边形ABCD,再代入四边形ABCD的面积即可得出结果.
解答 解:连接DG,BG,如图所示: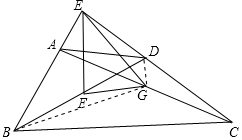
∵点G是AC中点,
∴S△AGD=S△CGD=$\frac{1}{2}$S△ACD,S△AGB=S△BGC=$\frac{1}{2}$S△ACB,
∵点F、G分别是BD、AC中点,
∴AG=GC,DF=FB,S△EGA=$\frac{1}{2}$S△EAC,S△FGB=$\frac{1}{2}$S△BDG,
S△BEF=$\frac{1}{2}$S△BED,
∴S△EFG=(S△EGA+S△AGB)-S△FGB-S△BEF,
S△EFG=($\frac{1}{2}$S△EAC+$\frac{1}{2}$S△ACB)-$\frac{1}{2}$S△BDG-$\frac{1}{2}$S△BED,
∴2S△EFG=S△EBC-S△BDG-S△BED=S△BGC+S△CGD,
即2S△GFE=$\frac{1}{2}$S△ACD+$\frac{1}{2}$S△ACB=$\frac{1}{2}$S四边形ABCD,
∴S△GFE=$\frac{1}{4}$S四边形ABCD=$\frac{1}{4}$×8068=2017.
点评 本题主要考查了面积及等积变换、三角形的中线的性质、中点的意义、面积的和差等知识;熟练掌握三角形的一条中线分成的两个三角形的面积相等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知实数a,b,c在数轴上的对应点如图所示,化简:$\root{3}{(a-b)^{3}}$-|b+c|-$\sqrt{(a-c)^{2}}$.
已知实数a,b,c在数轴上的对应点如图所示,化简:$\root{3}{(a-b)^{3}}$-|b+c|-$\sqrt{(a-c)^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
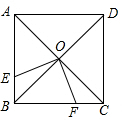 如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC上,且∠EOF=90°,则S四边形OEBF:S正方形ABCD=$\frac{1}{4}$.
如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC上,且∠EOF=90°,则S四边形OEBF:S正方形ABCD=$\frac{1}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com