
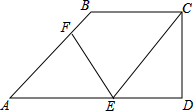
 在直角梯形ABCD中,AD∥BC,∠ADC=90°,AB=5,AD=8,CD=3,线段AD上有一动点E,过点E作EF⊥AB,垂足为点F.
在直角梯形ABCD中,AD∥BC,∠ADC=90°,AB=5,AD=8,CD=3,线段AD上有一动点E,过点E作EF⊥AB,垂足为点F.分析 (1)作BH⊥AE于H,如图,易得BH=CD=3,在Rt△ABH中利用勾股定理计算出AH=4,再证明Rt△AFE∽Rt△AHB,则利用相似比可计算出AE=$\frac{5}{2}$,然后利用DE=AD-AE进行计算即可;
(2)分类讨论:当△AEF∽△CED时,由于△AEF∽△ABH,则△CED∽△ABH,然后利用相似比可计算出DE;当△AEF∽△ECD时,由于△AEF∽△ABH,则△ECD∽△ABH,然后利用相似比可计算出DE.
解答 解:(1)作BH⊥AE于H,如图,
∵∠ADC=90°,
∴四边形BHDC为矩形,
∴BH=CD=3,
在Rt△ABH中,∵AB=5,BH=3,
∴AH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵∠FAE=∠HAB,
∴Rt△AFE∽Rt△AHB,
∴$\frac{AE}{AB}$=$\frac{AF}{AH}$,即$\frac{AE}{5}$=$\frac{2}{4}$,
∴AE=$\frac{5}{2}$,
∴DE=AD-AE=8-$\frac{5}{2}$=$\frac{11}{2}$;
(2)当△AEF∽△CED时,
∵△AEF∽△ABH,
∴△CED∽△ABH,
∴$\frac{DE}{BH}$=$\frac{CD}{AH}$,即$\frac{DE}{3}$=$\frac{3}{4}$,
∴DE=$\frac{9}{4}$;
当△AEF∽△ECD时,
∵△AEF∽△ABH,
∴△ECD∽△ABH,
∴$\frac{DE}{AH}$=$\frac{CD}{BH}$,即$\frac{DE}{4}$=$\frac{3}{3}$,
∴DE=4,
综上所述,DE的长为4或$\frac{9}{4}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用三角形相似的性质时,注意对应角相等.也考查了直角梯形.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,某小区有一块矩形空地,现将在这块矩形空地上设计一个菱形区域种植花草,且菱形的四个顶点落在矩形四条边上.利用尺规在下图中作出菱形的位置.
已知:如图,某小区有一块矩形空地,现将在这块矩形空地上设计一个菱形区域种植花草,且菱形的四个顶点落在矩形四条边上.利用尺规在下图中作出菱形的位置.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com