
【题目】定义:对角线互相垂直的凸四边形叫做“垂直四边形”.
(1)理解:
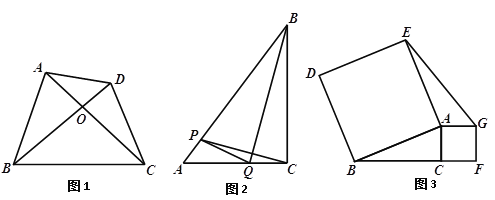
如图1,已知四边形ABCD是“垂直四边形”,对角线AC,BD交于点O,AC=8,BD=7,求四边形ABCD的面积.
(2)探究:
小明对 “垂直四边形”ABCD(如图1)进行了深入探究,发现其一组对边的平方和等于另一组对边的平方和.即![]() .你认为他的发现正确吗?试说明理由.
.你认为他的发现正确吗?试说明理由.
(3)应用:
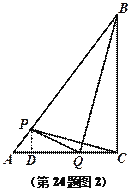
① 如图2,在△ABC中, ![]() ,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(
,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(![]() ),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
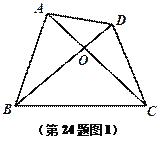
② 如图3,在△ABC中,![]() ,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
【答案】(1)28;(2)证明见解析;(3)①![]() ;②
;②![]()
【解析】试题分析:(1)由于对角线互相垂直,所以四边形ABCD的面积可化为![]() AOBD+
AOBD+![]() COBD的和;
COBD的和;
(2)由于对角线互相垂直,由勾股定理分别表示出AB2、CD2、AD2、BC2;
(3)①过点P作PD⊥AC于点D,构造△PAD∽△BAC后,利用BP2+CQ2=PQ2+BC2列出关于t的方程;②连接BE、CG、BG、CE,证明四边形BCGE是垂直四边形,然后利用其性质“一组对边的平方和等于另一组对边的平方和”,即可得出EG与BC的数量关系.
试题解析:(1)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD,
∴四边形ABCD的面积为![]() AOBD+
AOBD+![]() COBD=
COBD=![]() BD(AO+CO) =
BD(AO+CO) =![]() ACBD=
ACBD=![]() 2×8×7=28,
2×8×7=28,
故答案为:28;
(2)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD.
由勾股定理可知:
AB2+CD2=(AO2+BO2)+(DO2+CO2),
AD2+BC2=(AO2+DO2)+(BO2+CO2),
∴AB2+CD2=AD2+BC2;
(3)① 过点P作PD⊥AC于点D,
∵∠ACB=90°,
∴AB=![]() =10,PD∥BC.
=10,PD∥BC.
∴ △PAD∽△BAC,
∴![]() .
.
∵ 动点P的速度为每秒5个单位,动点Q的速度为每秒6个单位.
∴ AP=5t,CQ=6t
∴![]() ,∴AD=3t,PD=4t.
,∴AD=3t,PD=4t.
∵ 四边形BCQP是“垂直四边形”.
∴BP2+CQ2=PQ2+BC2.
∴(10-5t)2+(6t)2=(4t)2+(6-9t)2+82,
解得t=![]() 或t=0(舍去).
或t=0(舍去).
∴ 当四边形BCQP是“垂直四边形”时,t的值为![]() .
.
②如图3,
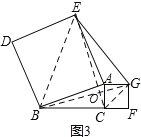
连接CG、BG、BE、CE,
CE与BG交于点O
由题意知:EA=BA,AC=AG
∠EAB=∠CAG=90°
∴∠EAB+∠BAC=∠CAG+∠BAC
∴∠EAC=∠BAG
在△EAC与△BAG中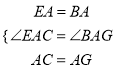 ,
,
∴△EAC≌△BAG(SAS)
∴∠CEA=∠GBA
∴∠EAB=∠BOE=90°
∴四边形BCGE是“垂直四边形”
∴BC2+EG2=BE2+CG2,
∵AB=3AC,
∴EG2=![]() BC2.
BC2.


科目:初中数学 来源: 题型:
【题目】如图1是流花河的水文资料(单位:米),取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?如表是小明记录的今年雨季流花河一周内水位变化情况(上周末的水位达到警戒水位)
星期 水位 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.2 | +0.8 | -0.4 | +0.1 | +0.3 | -0.4 | -0.1 |
实际水位/米 | 33.6 |
注:正表示水位比前一天上升,负表示水位比前一天下降.

(1)本周星期______河流的水位最高,水位在警戒水位之______(上或下);星期______河流的水位最低,水位在警戒水位之______(上或下);
(2)与上周相比,本周末河流水位是______(上升了或下降了);
(3)完成上面的实际水位记录;
(4)以警戒水位为0点,用折线统计图(如图2)表示本周的水位情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=5,BC=3,点D、E分别在BC、AC上,且BD=CE,设点C关于DE的对称点为F,若DF∥AB,则BD的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知二次函数y=x2-2x-3,请你化成y=(x-h)2+k的形式为____________,并在直角坐标系中画出y=x2-2x-3的图象;
(2)如果A(x1,y1),B(x2,y2)是(1)中图象上的两点,且x1<x2<1,请直接写出y1、y2的大小关系为___________;
(3)利用(1)中的图象表示出方程x2-2x-1=0的根来,要求保留画图痕迹,说明解题思路即可,不用计算结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.

(1)当a=-1,b=1时,求抛物线n的解析式;
(2)四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;
(3)若四边形AC1A1C为矩形,请求出a,b应满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化。从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果。所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人。
以下是根据我国近几年的人口相关数据制作的统计图和统计表。
2011-2014年全国人口年龄分布图

2011-2014年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0-14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15-64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
*以上图表中数据均为年末的数据。
根据以上材料解答下列问题:
(1)2011年末,我国总人口约为_______亿,全国人口年龄分布表中m的值为_______;
(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人。假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁的人口一直稳定在10亿,那么2027年末我国0-14岁人口约为_______亿,“老年人口抚养比”约为_______; (精确到1%)
(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子。在未来10年内,假设出生率显著提高,这_______(填“会”或“不会”)对我国的“老年人口抚养比”产生影响。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD为矩形,![]() ,
,![]() ,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.
,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.

(1)当点P在线段AB上运动了t秒时,![]() __________________(用代数式表示);
__________________(用代数式表示);
(2)t为何值时,四边形PDEB是平行四边形:
(3)在直线AB上是否存在点Q,使以D、E、Q、P四点为顶点的四边形是菱形?若存在,求出t的值:若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com