在△ABC中,∠ACB=90°,点D在直线BC上,BD=6,AD=BC,AC:CD=5:12.求S△ABD.
分析:设AC=5x,则CD=12x,根据勾股定理求得,AD=13x,因为AD=BC,所以BC=13x,
①点D在线段BC上时,BD=BC-CD=13x-12x=x=6,由此求出AC,CD,BC.而S
△ABD=S
△ABC-S
△ACD,把已知数据代入即可求出面积;②点D在线段BC外时,BD=BC+CD=13x+12x=25x=6,由此可以求出x,然后求出AC,CD,AD,BC,而S
△ABD=
BD•AC,直接代入数据即可求出结果.
解答:解:设AC=5x,则CD=12x,根据勾股定理求得,AD=13x,因为AD=BC,所以BC=13x,
①点D在线段BC上时,
BD=BC-CD=13x-12x=x=6,
则AC=30,CD=72,BC=78.
∴S
△ABD=S
△ABC-S
△ACD=
AC•BC-
AC•CD=
×30×78-
×30×72=90;
②点D在线段BC外时,
BD=BC+CD=13x+12x=25x=6,则x=
,
∴AC=
,CD=
,AD=BC=
,
∴S
△ABD=
BD•AC=
×6×
=
.
点评:因为点D在直线BC上,所以两种情况应该考虑到:(1)点D在线段BC上;(2)点D在线段BC外.此题主要用到了勾股定理、三角形的面积公式等知识点.



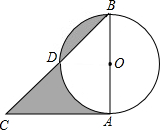 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=