
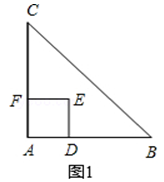

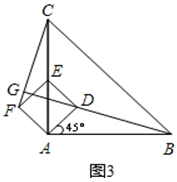
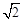 时,求线段FG的长.
时,求线段FG的长.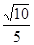 .
.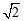 , AN="1," CN=3,由勾股定理CF=
, AN="1," CN=3,由勾股定理CF=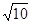 ,设FG=x,CG=
,设FG=x,CG=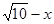 ,在Rt△FGD中,∵FD=2,∴GD=
,在Rt△FGD中,∵FD=2,∴GD=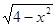 ,∵在Rt△BCG中,
,∵在Rt△BCG中,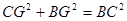 ,
,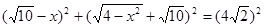 ,解之得FG=
,解之得FG=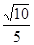 .
.
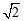 ,
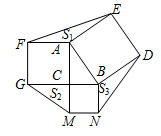
,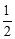 AE=1,FD=2,
AE=1,FD=2, ,
,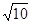 ,
,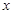 ,在Rt△FGD中,∵FD=2,∴GD=
,在Rt△FGD中,∵FD=2,∴GD=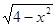 ,
,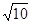 ,∴CG=
,∴CG=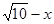 ,
, ,
,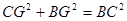 ,
,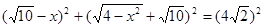 ,
, 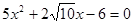 ,
,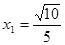 ,
,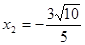 (不合题意,故舍去)
(不合题意,故舍去)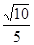 .
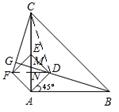
.
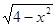 ,CG=
,CG=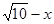 ,
, 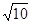 ,
, 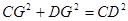 ,即
,即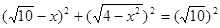
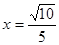 ,故FG=
,故FG=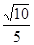 .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题: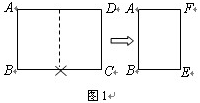

 ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.一组对边平行的四边形是平行四边形 |
| B.两条对角线相等的平行四边形是矩形 |
| C.两边相等的平行四边形是菱形 |
| D.对角线互相垂直且相等的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
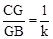 ,则
,则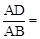 (用含k的代数式表示).
(用含k的代数式表示).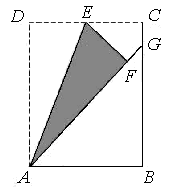
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com