
 如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点A,若AM:MN=2:3,则k=$\frac{10}{3}$.
如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点A,若AM:MN=2:3,则k=$\frac{10}{3}$. 分析 过点A作AB⊥x轴于点B,通过AB∥MO找出△NMO∽△NAB,根据相似三角形的性质找出$\frac{MO}{AB}=\frac{NO}{NB}=\frac{NM}{NA}$,再根据AM:MN=2:3以及OM=3可求出AB的长度,由此即可得出点A的坐标,结合点A的坐标利用待定系数法即可求出k值.
解答 解:过点A作AB⊥x轴于点B,如图所示.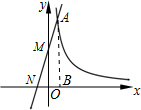
∵AB⊥x轴,MO⊥x轴,
∴AB∥MO,
∴△NMO∽△NAB,
∴$\frac{MO}{AB}=\frac{NO}{NB}=\frac{NM}{NA}$.
∵AM:MN=2:3,
MN:AN=3:(2+3)=3:5.
令一次函数y=kx+3中x=0,则y=3,
∴MO=3.
∵$\frac{MO}{AB}=\frac{NM}{NA}$=$\frac{3}{5}$,
∴AB=5,
令反比例函数y=$\frac{3}{x}$中y=5,则5=$\frac{3}{x}$,
解得:x=$\frac{3}{5}$.
∴点A的坐标为($\frac{3}{5}$,5).
将点A($\frac{3}{5}$,5)代入一次函数y=kx+3中,
得:5=$\frac{3}{5}$k+3,解得:k=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题、相似三角形的判定及性质以及待定系数法求函数解析式,解题的关键是求出点A的坐标.本题属于基础题,难度不大,解决该题型题目时,求出点的坐标,再利用待定系数法求出函数解析式是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| A | B | C | D | |
| A | ||||
| B | ||||
| C | ||||
| D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
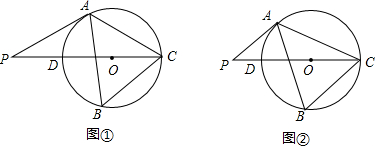
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
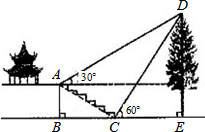 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
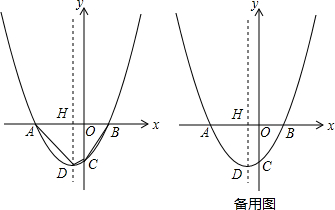
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com