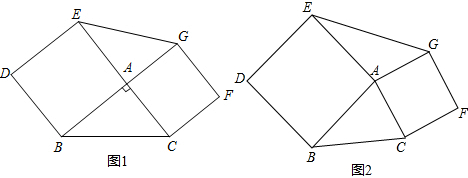
解:(1)S
△ABC=S
△AEG;
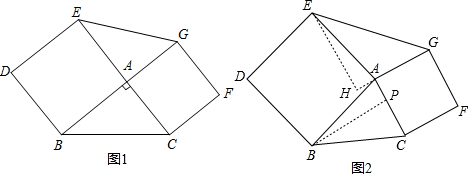
理由:∵四边形ABDE和四边形ACFG都是正方形,
∴AE=AB,AG=AC,∠EAB=∠GAC=90°,
∵AC,AE在同一条直线上,
∴∠EAB+∠BAC=180°,
∴∠BAC=90°.
∵∠EAB+∠GAC+∠BAC+∠EAG=360°,
∴∠EAG=90°,
∴∠BAC=∠EAG.
在△ABC和△AEG中
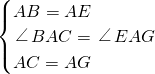
∴△ABC≌△AEG(SAS),
∴S
△ABC=S
△AEG;
(2)S
△ABC=S
△AEG成立.
理由:作AH⊥GA交GA的延长线于点H,作BP⊥AC于点P,
∴∠AHE=∠APB=90°.
∵四边形ABDE和四边形ACFG都是正方形,
∴AE=AB,AG=AC,∠EAB=∠GAC=90°,
∵∠EAB+∠GAC+∠BAC+∠EAG=360°,
∴∠EAG+∠BAC=180°.
∵∠EAG+∠EAH=180°,
∴∠EAH=∠BAP.
在△AHE和△APB中

,
∴△AHE≌△APB(AAS),
∴EH=BP.
∵AG=AC,
∴

AG.EH=

AC.BP,
∴S
△ABC=S
△AEG.
分析:(1)根据正方形的性质可以得出△ABC≌△AEG,就可以得出S
△ABC=S
△AEG;
(2)作AH⊥GA交GA的延长线于点H,作BP⊥AC于点P,证明△AHE≌△APB就可以得出EH=BP,就可以得出结论.
点评:本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,三角形的面积公式的运用,解答时证明三角形全等是关键.


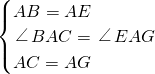
 ,
, AG.EH=
AG.EH= AC.BP,
AC.BP,

 小学课时特训系列答案
小学课时特训系列答案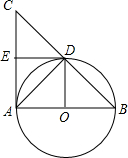 (2012•广州模拟)如图,以△ABC的边AB为直径的⊙O交边BC于点D,其中边AC与⊙O相切于点A,E为AC中点.
(2012•广州模拟)如图,以△ABC的边AB为直径的⊙O交边BC于点D,其中边AC与⊙O相切于点A,E为AC中点.