
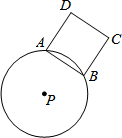
 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π. 分析 连接PD,过点P作PE⊥CD与点E,PE交AB于点F,则CD边扫过的面积为以PD为外圆半径、PE为内圆半径的圆环面积,利用垂径定理即可得出AF=BF,进而可得出DE=CE=3,再根据圆环的面积公式结合勾股定理即可得出CD边扫过的面积.
解答 解:连接PD,过点P作PE⊥CD与点E,PE交AB于点F,则CD边扫过的面积为以PD为外圆半径、PE为内圆半径的圆环面积,如图所示.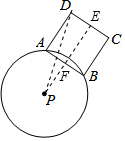
∵PE⊥CD,AB∥CD,
∴PF⊥AB.
又∵AB为⊙P的弦,
∴AF=BF,
∴DE=CE=$\frac{1}{2}$CD=$\frac{1}{2}$AB=3,
∴CD边扫过的面积为π(PD2-PE2)=π•DE2=9π.
故答案为:9π.
点评 本题考查了垂径定理、勾股定理、平行线的性质以及圆环的面积公式,结合AB边的旋转,找出CD边旋转过程中扫过区域的形状是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.
实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
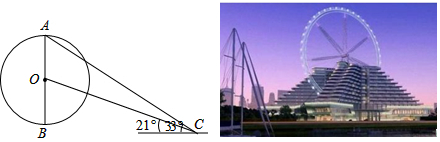
| A. | 169米 | B. | 204米 | C. | 240米 | D. | 407米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
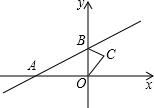 如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).
如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com