
 有一个附有进出水管的容器,每单位时间内进出的水量都是一定的,设从某时
有一个附有进出水管的容器,每单位时间内进出的水量都是一定的,设从某时分析 (1)由图形可以看出每分钟的进水量;
(2)由两点式可以写出函数关系式;
(3)先求出每分钟放水量,然后求出放水需要的时间,找出两坐标点,列出函数关系式.
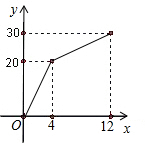
解答 解:(1)由图形可以看出在0到4分钟进水20升,故每分钟进水5升;
(2)知道两点(4,20)、(12,30),由两点式写出函数关系式为:
y=$\frac{5}{4}$x+15;
(3)设每分钟出水量为a升.在4到12分钟的图形可知,
5×8-8a=10,
解得a=$\frac{15}{4}$,故需要8分钟放完水.
由图象可知两点(12,30)、(20,0),
由两点式求函数关系式为y=-$\frac{15}{4}$x+75.
点评 本题主要考查一次函数的应用,会求一次函数的解析式,看懂图形是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
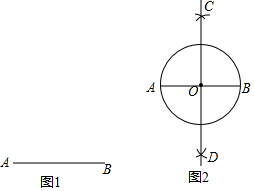 下面是“以已知线段为直径作圆”的尺规作图过程.
下面是“以已知线段为直径作圆”的尺规作图过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=(m+2)x2-2(m+2)x-m+5,其中m+2>0.
二次函数y=(m+2)x2-2(m+2)x-m+5,其中m+2>0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.| x | … | -3 | -2 | -1 | 0 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | 2 | $\frac{9}{4}$ | $\frac{8}{3}$ | $\frac{25}{8}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com