练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（　　）
    A．a=2bB．a=3bC．a=4bD．a=b

    分析 表示出左上角与右下角部分的面积，求出之差，根据差与BC无关即可求出a与b的关系式．

    解答 解：左上角阴影部分的长为AE，宽为AF=a，右下角阴影部分的长为PC，宽为2b，
    ∵AD=BC，即AE+ED=AE+4b，BC=BP+PC=a+PC
    ∴AE+4b=a+PC，
    ∴AE=a-4b+PC，
    ∴阴影部分面积之差S=AE•AF-PC•CG=aAE-2bPC=a（a-4b+PC）-2bPC=（a-2b）PC+a2-4ab，
    则a-2b=0，即a=2b．
    故选A．

    点评 此题考查了整式的混合运算的应用，弄清题意是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．对于实数a、，b，定义运算?如下：a?b=$\left\{\begin{array}{l}{{a}^{b}（a＞b，a≠0）}\\{{a}^{-b}（a≤b，a≠0）}\end{array}\right.$，例如：2?4=2-4=$\frac{1}{16}$，计算[2?2]×[3?2]=$\frac{9}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

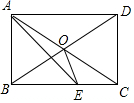    18．在矩形ABCD中，AC和BD交于点O，∠AOB=60°，AE平分∠BAD交BC于E，则∠BOE的度数为（　　）
    A．60°B．65°C．70°D．75°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，面积为28的平行四边形纸片ABCD中，AB=7，∠BAD=45°，按下列步骤进行裁剪和拼图．

    第一步：如图①，将平行四边形纸片沿对角线BD剪开，得到△ABD和△BCD纸片，再将△ABD纸片沿AE剪开（E为BD上任意一点），得到△ABE和△ADE纸片；
    第二步：如图②，将△ABE纸片平移至△DCF处，将△ADE纸片平移至△BCG处；
    第三步：如图③，将△DCF纸片翻转过来使其背面朝上置于△PQM处（边PQ与DC重合，△PQM和△DCF在DC同侧），将△BCG纸片翻转过来使其背面朝上置于△PRN处，（边PR与BC重合，△PRN和△BCG在BC同侧）．则由纸片拼成的五边形PMQRN中，对角线MN长度的最小值为$\frac{28}{5}\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．将边长为acm的正方形的边长增加4cm后，所得新正方形的面积比原正方形的面积大（　　）
    A．4acm2B．（4a+16）cm2C．8acm2D．（8a+16）cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠ACB、∠DCB、∠EDC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图1，在正方形ABCD中，P为对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F，连接CE．
    （1）求证：△PCE是等腰直角三角形；
    （2）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，判断△PCE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某服装厂生产一种夹克和T恤，夹克每件定价100元，T恤每件定价50元．厂方在开展促销活动期间，向客户提供两种优惠方案：①买一件夹克送一件T恤；
    ②夹克和T恤都按定价的80%付款．
    现某客户要到该服装厂购买夹克30件，T恤件（x＞30）．
    （1）若该客户按方案①购买需付款1500+50x元（用含x的式子表示）；
    若该客户按方案②购买需付款2400+40x元（用含x的式子表示）；
    （2）若x=50时，通过计算说明按方案①、方案②哪种方案购买较为合算？
    （3）当x=50时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知直线y=$\frac{-（n+1）}{n+2}$x+$\frac{1}{n+2}$（n为正整数）与坐标轴围成的三角形的面积是Sn，则S1+S2+S3+…+S2016=$\frac{1009}{4036}$．

    查看答案和解析>>

    同步练习册答案