
分析 先根据算术平方根和偶次方的非负性求出x、y的值,再算乘法,合并同类项,最后算除法,代入后求出即可.
解答 解:$\sqrt{x+\frac{1}{2}}+{y^2}+9-6y$=0,
$\sqrt{x+\frac{1}{2}}$+(y-3)2=0,
x+$\frac{1}{2}$=0,y-3=0,
x=-$\frac{1}{2}$,y=3,
[(x-2y)2+(x-y)(x+4y)-2x(2x-y)]÷2x
=[x2-4xy+4y2+x2+4xy-xy-4y2-4x2+2xy]÷2x
=(-2x2+xy)÷2x
=$-x+\frac{y}{2}$=2.
点评 本题考查了整式的混合运算和求值,算术平方根、偶次方的非负性的应用,解此题的关键是求出x、y的值和能根据整式的运算法则进行化简,难度适中.


科目:初中数学 来源: 题型:解答题
 如图,直线y=kx与双曲线y=$\frac{m}{x}$相交于A,B两点,点A在第一象限,过点A作AC⊥y轴,垂足为点C,若AC=1,△BOC的面积是1,解答下列问题:
如图,直线y=kx与双曲线y=$\frac{m}{x}$相交于A,B两点,点A在第一象限,过点A作AC⊥y轴,垂足为点C,若AC=1,△BOC的面积是1,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-2,b),B两点.
如图,一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-2,b),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | $\sqrt{3}$ | C. | 3 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
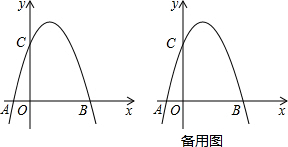
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
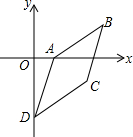 已知平行四边形ABCD中,A(2,0)、B(6,4)、D(0,-6)
已知平行四边形ABCD中,A(2,0)、B(6,4)、D(0,-6)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com