
【题目】实践与探究
在平面直角坐标系中,四边形AOBC是矩形,点![]() (0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
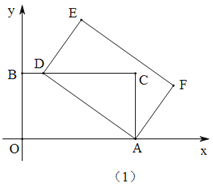
(1)如图(1),当点D落在BC边上时,求点D的坐标;
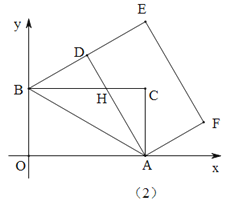
(2)如图(2),当点D落在线段BE上时,AD与BC交于点H.
①求证:ΔADB≌ΔAOB;
②求点H的坐标.
【答案】(1)D(1,3);(2)①证明见解析;②H(![]() ,3).
,3).
【解析】
(1)如图①,在Rt△ACD中,根据勾股定理求出CD,即可解决问题;
(2)①根据旋转可知,OA=DA,则根据HL证明全等即可;
②先证明△BDH≌△ACH,得DH=CH,设CH=x,则AH =5-x,在Rt△AHC中,根据AH2=HC2+AC2,构建方程求出x即可解决问题;
解:(1)∵A(5,0),B(0,3),
∴OA=5,OB=3,
∵四边形AOBC是矩形,
∴OB=AC=3,OA=BC=5 ∠C=90°,
∵矩形ADEF是由矩形AOBC旋转得到的,
∴AD=OA=5 .
在RtΔACD中
CD=![]() ,
,
∴BD=1,
∴D(1,3) .
(2)①由旋转可知:
OA=DA,∠AOB=∠ADE=90°,
∴∠AOB=∠ADB=90°,
在Rt△AOB与Rt△ADB中
![]() ,
,
∴△ADB≌△AOB(HL);
②∵△ADB≌△AOB(HL),
∴BD=BO=AC ,
在△BDH与△ACH中
 ,
,
∴△BDH≌△ACH(AAS),
∴DH=CH,
∵DH+AH=AD=5,
∴CH+AH=5,
设CH=![]() ,则AH=
,则AH=![]() ,
,
在Rt△ACH中
![]() ,
,
解得:![]() ,
,
∴BH=![]() ,
,
∴H(![]() ,3).
,3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的一角![]() 两边为边,用总长为
两边为边,用总长为![]() 的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且这三块区域的面积相等,四边形
的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且这三块区域的面积相等,四边形![]() 为直角梯形.
为直角梯形.
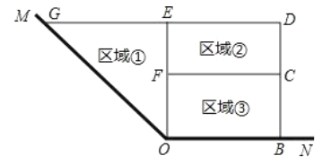
(1)设![]() 的长度为
的长度为![]() ,则
,则![]() 的长为______
的长为______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并注明自变量
之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(3)![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ的面积是![]() cm2;
cm2;
(3)直接写出t为何值时,△BPQ是等腰三角形;
(4)连接AQ,CP,若AQ⊥CP,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
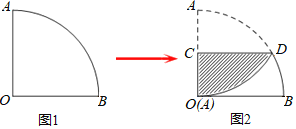
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为_____.(答案用根号表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小阳,小杰和小凡到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为10元/千克,下面是他们在活动结束后的对话.
小阳:如果以12元/千克的价格销售,那么每天可售出300千克.
小杰:如果以15元/千克的价格销售,那么每天可获取利润750元.
小凡:我通过调查验证发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获得的利润达600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,
![]()
使∠ACB=30°。(利用直尺和圆规作图,保留作图痕迹,不写作法).
尝试解决:为了解决这个问题,下面给出一种解题思路:先作出等边三角形AOB,然后以点O 为圆心,OA长为半径作⊙O,则优弧AB上的点即为所要求作的点(点A、B除外),根据对称性,在AB的另一侧符合条件的点C易得。请根据提示,完成作图.
自主探索:在平面直角坐标系中,已知点A(3,0)、B(-1,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() 交边
交边![]() 于点
于点![]() .
.

(1)当点![]() 与
与![]() 恰好重合时(如图1),求
恰好重合时(如图1),求![]() 的长;
的长;
(2)问:是否可能使![]() 、
、![]() 与
与![]() 都相似?若能,请求出此时
都相似?若能,请求出此时![]() 的长;若不能,请说明理由(如图2).
的长;若不能,请说明理由(如图2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
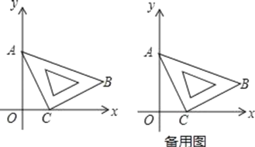
(1)直接写出点B的坐标是 ;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
(4)在x轴上方,抛物线l上是否存在一点P,使由点A,C,B,P构成的四边形为中心对称图形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com