
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于原点O和点A(6,0),抛物线的顶点为B.
x2+bx+c与x轴交于原点O和点A(6,0),抛物线的顶点为B.

(1)求该抛物线的解析式和顶点B的坐标;
(2)若动点P从原点O出发,以每秒1个长度单位的速度沿线段OB运动,设点P运动的时间为t(s).问当t为何值时,△OPA是直角三角形?
(3)若同时有一动点M从点A出发,以2个长度单位的速度沿线段AO运动,当P、M其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t(s),连接MP,当t为何值时,四边形ABPM的面积最小?并求此最小值.
【答案】(1)y=﹣![]() x2+2
x2+2![]() x,(3,3
x,(3,3![]() );(2)t=3时,△OPA是直角三角形;(3)当t=
);(2)t=3时,△OPA是直角三角形;(3)当t=![]() 时,四边形ABPM的面积取最小值,最小值为
时,四边形ABPM的面积取最小值,最小值为![]()
【解析】
(1)根据点O,A的坐标,利用待定系数法可求出二次函数的解析式,再将二次函数解析式由一般式变形为顶点式,即可得出顶点B的坐标;
(2)由点B的坐标,利用待定系数法可求出直线OB的解析式,过点P作PC⊥x轴于点C,设点P的坐标为(x,![]() x),则点C的坐标为(x,0),由tan∠POC=
x),则点C的坐标为(x,0),由tan∠POC=![]() 可得出∠POC=60°,结合OA的值可找出当∠APO=90°时OP的长,由点P的运动速度为1可求出此时t的值;
可得出∠POC=60°,结合OA的值可找出当∠APO=90°时OP的长,由点P的运动速度为1可求出此时t的值;
(3)当运动时间为t时,OP=t,AM=2t,PC=![]() t,PC=
t,PC=![]() t,OM=6﹣2t,结合点P,M的运动速度可得出0≤t≤3,由S四边形ABPM=S△ABO﹣S△POM可得出四边形ABPM的面积关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
t,OM=6﹣2t,结合点P,M的运动速度可得出0≤t≤3,由S四边形ABPM=S△ABO﹣S△POM可得出四边形ABPM的面积关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
解:(1)将O(0,0),A(6,0)代入y=﹣![]() x2+bx+c,得:
x2+bx+c,得:
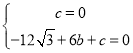 ,解得:
,解得: ,
,
∴该抛物线的解析式为y=﹣![]() x2+2
x2+2![]() x.
x.
∵y=﹣![]() x2+2
x2+2![]() x=﹣
x=﹣![]() (x﹣3)2+3
(x﹣3)2+3![]() ,
,
∴顶点B的坐标为(3,3![]() ).
).
(2)设直线OB的解析式为y=kx,
将B(3,3![]() )代入y=kx,得:3
)代入y=kx,得:3![]() =3k,
=3k,
解得:k=![]() ,
,
∴直线OB的解析式为y=![]() x.
x.
过点P作PC⊥x轴于点C,如图1所示.

设点P的坐标为(x,![]() x),则点C的坐标为(x,0).
x),则点C的坐标为(x,0).
∵tan∠POC=![]() =
=![]() ,
,
∴∠POC=60°.
当∠APO=90°,则cos∠POC=![]() =
=![]() ,
,
∴OP=3.
∵OP=1×t=3,
∴t=3.
(3)当运动时间为t时,OP=t,AM=2t,PC=![]() t,PC=
t,PC=![]() t,OM=6﹣2t.
t,OM=6﹣2t.
∵当P、M其中一个点停止运动时另一个点也随之停止运动,
∴0≤t≤3.
S四边形ABPM=S△ABO﹣S△POM,
=![]() OAyB﹣
OAyB﹣![]() OMPC,
OMPC,
=![]() ×6×3
×6×3![]() ﹣
﹣![]() ×(6﹣2t)×
×(6﹣2t)×![]() t,
t,
=![]() t2﹣
t2﹣![]() t+9
t+9![]() ,
,
=![]() (t﹣
(t﹣![]() )2+
)2+![]() .
.
∵![]() >0,
>0,
∴当t=![]() 时,四边形ABPM的面积取最小值,最小值为
时,四边形ABPM的面积取最小值,最小值为![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
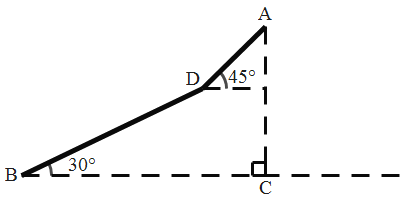
【题目】某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=308米,步行道BD=336米,∠DBC=30°,在D处测得山顶A的仰角为45°,求电动扶梯DA的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有5个分别标有数字1,2,3,4,5的小球,它们的形状、大小、质地等完全相同.雄威同学先从盒子里随机取出第一个小球,记下数字为x;不放回盒子,再由丽贤同学随机取出第二个小球,记下数字为y.
(1)请用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;
(2)求雄威同学、丽贤同学各取一个小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转![]() 得到线段PE,连接AE,BP,CE.
得到线段PE,连接AE,BP,CE.
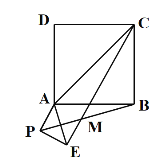
(1)求证:![]() ;
;
(2)当线段BP与CE相交时,设交点为M,求![]() 的值以及
的值以及![]() 的度数;
的度数;
(3)若正方形ABCD的边长为3,![]() ,当点P,C,E在同一直线上时,求线段BP的长.
,当点P,C,E在同一直线上时,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
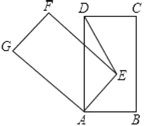
【题目】如图,将一个8cm×16cm智屏手机抽象成一个的矩形ABCD,其中AB=8cm,AD=16cm,然后将它围绕顶点A逆时针旋转一周,旋转过程中A、B、C、D的对应点依次为A、E、F、G,则当△ADE为直角三角形时,若旋转角为α(0<α<360°),则α的大小为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,7个腰长为1的等腰直角三角形(Rt△B1AA1,Rt△B2A1A2,Rt△B3A2A3…)有一条腰在同一条直线上,设△A1B2C1的面积为S1,△A2B3C2的面积为S2,△A3B4C3的面积为S3,则阴影部分的面积是______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在“书香校园”活动中,为了解学生的读书情况,学校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
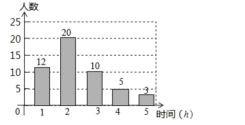
(1)被抽查学生阅读时间的中位数为____h,平均数为_____h;
(2)若该校共有2000名学生,请你估算该校一周内阅读时间不少于3h的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com