
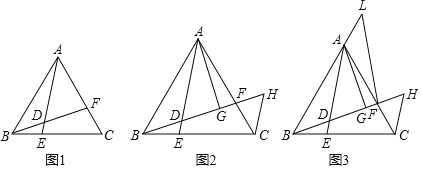
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
【答案】(1)证明见解析;(2)BH:CH=![]() ;(3)△ABC的面积为9.
;(3)△ABC的面积为9.
【解析】
(1)根据等边三角形的性质得到AB=BC,∠ABC=∠C,证明△ABE≌△BCF,根据全等三角形的性质,得到答案;
(2)连接CG,证明△ABD≌△BCG(SAS),得BD=CG,∠ADB=∠BGC=120![]() ,根据平行线的性质得∠H=∠ADG=60
,根据平行线的性质得∠H=∠ADG=60![]() ,证明△CGH是等边三角形,得BH=3BD=3CH,得结论;
,证明△CGH是等边三角形,得BH=3BD=3CH,得结论;
(3)如图3,作辅助线,构建高线FM,设CF=a,证明△BCF∽△BHC,![]() ,根据同高三角形面积的比为对应底边的比.
,根据同高三角形面积的比为对应底边的比.
(1)如图1.
∵三角形ABC是等边三角形,

∴AB=BC,∠ABE=∠BCF=60![]() ,
,
在△ABE和△BCF中,
 ,
,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)如图2,由(1)得:△ABE≌△BCF,
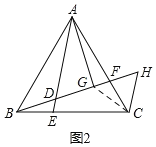
∴∠BAE=∠CBF.
∵∠ADG=∠ABD+∠BAE,
∴∠ADG=∠ABD+∠CBF=∠ABC=60![]() ,
,
∴∠ADB=120![]() .
.
∵AG⊥BH,
∴∠DAG=30![]() ,
,
∴DG=![]() AD.
AD.
∵D为BG中点,
∴BD=DG=![]() BG,
BG,
∴AD=BG,
连接CG,如图2所示:
在△ABD和△BCG中,
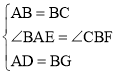 ,
,
∴△ABD≌△BCG(SAS),
∴BD=CG,∠ADB=∠BGC=120![]() ,
,
∴∠CGH=60![]() .
.
∵CH∥AE,
∴∠H=∠ADG=60![]() ,
,
∴∠CGH=∠H=60![]() ,
,
∴△CGH是等边三角形,
∴GH=CH=CG=BD,
∴BH=3BD=3CH,
∴BH:CH=![]() ;
;
(3)如图3,由(2)知:∠H=∠ADF=60![]() ,
,
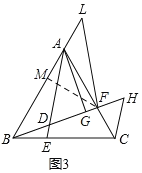
∴∠BCF=∠H=60![]() ,∠CBF=∠CBH,
,∠CBF=∠CBH,
∴△BCF∽△BHC,
∴![]() ,
,
设CF=a,则BC=3a,AF=2a,
过F作FM⊥AB于M,
Rt△AFM中,∠FAM=60![]() ,∴∠AFM=30
,∴∠AFM=30![]() ,∴AM=a,FM=
,∴AM=a,FM=![]() a,
a,
∴BM=3a﹣a=2a.
∵BF=FL,
∴LM=BM=2a,
∴AL=a,
∴![]() =
=![]() .
.
∵△FLA的面积为2,
∴△ABF的面积为6.
∵![]()
∴△ABC的面积为9.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
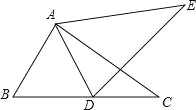
【题目】已知:如图,点B、D、C在一条直线上,AB=AD,BC=DE,AC=AE,
(1)求证:∠EAC=∠BAD.
(2)若∠BAD=42°,求∠EDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
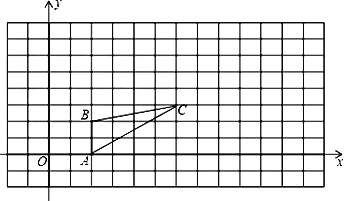
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1) 请在图中画出一个△![]() ,使△
,使△![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
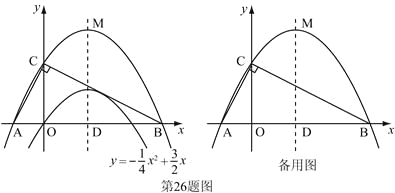
【题目】(本题满分12分)已知二次函数![]() 的图象如图.
的图象如图.
(1)求它的对称轴与![]() 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与![]() 轴,
轴,![]() 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() 的顶点
的顶点![]() 是底边
是底边![]() 的中点,两边分别与
的中点,两边分别与![]() 交于点
交于点![]() .
.
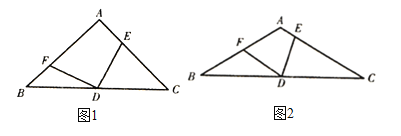
(1)如图1,![]() ,当
,当![]() 的位置变化时,
的位置变化时,![]() 是否随之变化?证明你的结论;
是否随之变化?证明你的结论;
(2)如图2,当![]() ,当
,当![]() °时,(1)中的结论仍然成立,求出此时
°时,(1)中的结论仍然成立,求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)÷4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA。
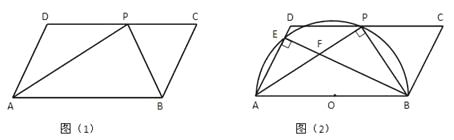
【1】判断△APB是什么三角形?证明你的结论;
【2】比较DP与PC的大小;
【3】如图(2)以AB为直径作半圆O,交AD于点E,连结BE与AP交于点F,若AD=5cm,AP=8cm,求证△AEF∽△APB,并求tan∠AFE的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com