

分析 (1)过点P作AD的垂线,交AD于点E,交BC于点F,可证四边形ABFE和CDEF为矩形,则AE=BF,DE=CF,在△PAE,△PCF,△PBF,△PCF中,分别求PA2,PC2,PB2,PD2,再比较PA2+PC2与PB2+PD2即可;
(2)根据PB2-PA2=AB2=CD2=PC2-PD2,移项即可;
(3)画出图形,把问题转化到直角三角形中,由勾股定理分别求PA2,PC2,PB2,PD2.
解答  (1)证明:过点P作AD的垂线,交AD于点E,交BC于点F,如图(a)所示:
(1)证明:过点P作AD的垂线,交AD于点E,交BC于点F,如图(a)所示:
则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
(2)成立,理由如下:在Rt△ABP中,由勾股定理,得PB2-PA2=AB2,
同理可得PC2-PD2=CD2,
由矩形的性质可得AB=CD,
∴PB2-PA2=PC2-PD2,
∴PA2+PC2=PB2+PD2.
(2)成立
过点P作AD的垂线,交AD于点E,交BC于点F,
则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得: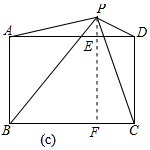
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2
∴PA2+PC2=PB2+PD2.
(3)成立.如图(c)所示,由勾股定理可证PA2+PC2=PB2+PD2.
点评 本题是四边形综合题目,考查了勾股定理及矩形的性质.关键是作辅助线,构造直角三角形,利用勾股定理分别表示边长的平方.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,实验数据显示,一般成年人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可以近似的用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似的用反比例函数y=$\frac{k}{x}$(k>0)刻画.
如图,实验数据显示,一般成年人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可以近似的用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似的用反比例函数y=$\frac{k}{x}$(k>0)刻画.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
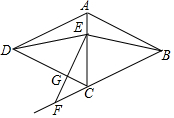 如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,
如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 18 | 19 | 20 | 21 | 22 |
| 人数 | 2 | 5 | 2 | 2 | 1 |
| A. | 2,20岁 | B. | 2,19岁 | C. | 19岁,20岁 | D. | 19岁,19岁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com