
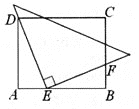
【题目】如图,在矩形ABCD中,AD=6,AB=10,一个三角形的直角顶点E是边AB上的一动点,一直角边过点D,另一直角边与BC交于F,若AE=x,BF=y,则y关于x的函数关系的图象大致为( )
A.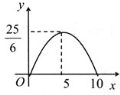 B.
B.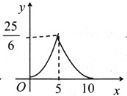 C.
C.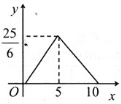 D.
D.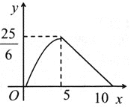
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房的成交均价由2019年8月份的8000元/![]() 下降到2019年10月份的7500元/
下降到2019年10月份的7500元/![]() .
.
(1)求2019年9、10两月该市的商品房成交均价平均每月降价的百分率(精确到0.1,参考数据:![]() );
);
(2)如果房价继续回落,按(1)的降价的百分率,你认为到2019年12月份该市的商品房成交均价会跌破7000元/![]() 吗?请说明理由.
吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场服装柜在销售中发现:某牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现,如果每件童装每降价4元,那么平均每天就可多售出8件,
(1)若商场要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
(2)若商场要想平均每天在销售这种童装上盈利最多,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△CDE是以点C为公共顶点的两个三角形.

(1)如图1,当AB=AC,CD=CE,∠BAC=∠DCE=90°时,连接BD,取BD的中点M,连接AM.探究AM、BE之间的数量关系,并证明你的结论;
(2)如图2,当AB=AC,∠BAC=120°,∠CDE=60°,∠DCE=90°时,连接BD,取BD的中点M,连接AM.探究AM、BE之间的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=53°,且DE=2.4米,求匾额悬挂的高度AB的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学利用寒假30天时间贩卖草莓,了解到某品种草莓成本为10元/千克,在第![]() 天的销售量与销售单价如下(每天内单价和销售量保持一致):
天的销售量与销售单价如下(每天内单价和销售量保持一致):
销售量 |
|
销售单价 | 当 |
当 |
设第![]() 天的利润
天的利润![]() 元.
元.
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?注:利润=(售价-成本)×销售量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() 的图象相交于点A,并与
的图象相交于点A,并与![]() 轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
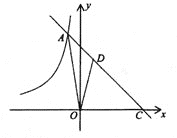
(1)求![]() 的值;
的值;
(2)求点D的坐标;
(3)根据图象,直接写出当![]() 时不等式
时不等式![]() 的
的![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数t=![]() (其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.
(其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.
(1)根据以上方法求出T(268)= ,T(513)= ;
(2)已知三位数![]() (其中a>b>1)的差数T(
(其中a>b>1)的差数T(![]() )=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.
)=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com