
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

【答案】(1)ECF=![]() ;
;
(2)证明见解析;
(3)结论:当O=60时 ,CD平分OCF,理由见解析.
【解析】试题分析:由两直线平行,同位角相等得∠ACE =40,由平角定义得∠ACD=![]() ,再由角平分线定义得
,再由角平分线定义得![]() ,由邻补角定义得到ECF=
,由邻补角定义得到ECF=![]() ;(2)由垂直的定义得
;(2)由垂直的定义得![]() ,由
,由![]() 得
得![]() ,由等角的余角相等可证;(3)由两直线平行,同位角相等得∠DCO=∠O=60,由角平分线性质得∠DCF=60,由等量代换得
,由等角的余角相等可证;(3)由两直线平行,同位角相等得∠DCO=∠O=60,由角平分线性质得∠DCF=60,由等量代换得![]() 即可得证.
即可得证.
试题解析:(1)∵DE//OB ,
∴∠O=∠ACE,(两直线平行,同位角相等)
∵O =40,
∴∠ACE =40,
∵∠ACD+∠ACE=![]() (平角定义)
(平角定义)
∴ ∠ACD=![]()
又 ∵CF平分ACD ,
∴![]() (角平分线定义)
(角平分线定义)
∴ ECF=![]()
(2)证明:∵CG CF,
∴![]() .
.
∴![]()
又 ∵![]()
![]() )
)
∴![]()
∵![]()
∴![]() (等角的余角相等)
(等角的余角相等)
即CG平分OCD .
(3)结论:当O=60时 ,CD平分OCF .
当O=60时
∵DE//OB,
∴ ∠DCO=∠O=60.
∴ ∠ACD=120.
又 ∵CF平分ACD
∴ ∠DCF=60,
∴![]()
即CD平分OCF .


科目:初中数学 来源: 题型:
【题目】“在山区建设公路时,时常要打通一条隧道,就能缩短路程”,其中蕴含的数学道理是( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点,有无数条直线 D. 连接两点之间的线段的长度是两点间的距离
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用网格画图:
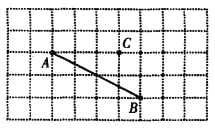
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
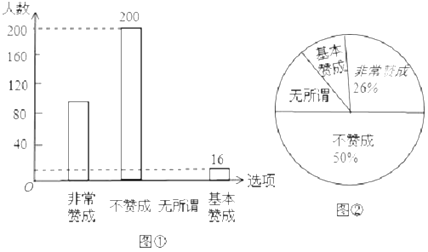
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)若该学校有2000名家长,请根据该统计结果估算表示“基本赞成”的家长有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
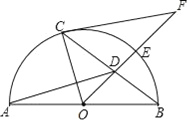
【题目】如图,AB是半圆O上的直径,E是![]() 的中点,OE交弦BC于点D,过点C作⊙O的切线交OE的延长线于点F,已知BC=8,DE=2.
的中点,OE交弦BC于点D,过点C作⊙O的切线交OE的延长线于点F,已知BC=8,DE=2.
(1)求⊙O的半径;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“滴滴”已成为一种出行习惯,其中的“滴滴专车”正成为非常热门的出行选择.经了解温州地区滴滴专车部分计价规则如下表:
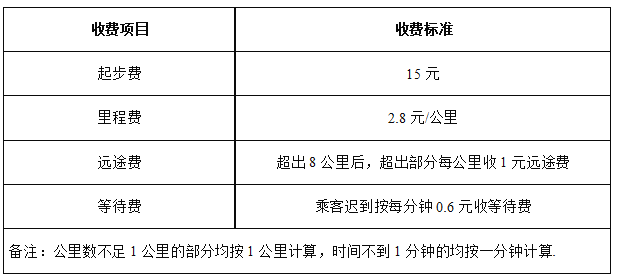
以没有收取等待费为例:某甲坐车10公里的费用为15+2.8×10+1×(10-8)=45元
(1)若行驶里程为6千米,且没有收取等待费,求应支付的总费用;
(2)若某天小周迟到7分钟才上车,且里程数超过了8公里,最终支付的总费用为53元,求支付的远途费;
(3)某次行程结束后,乘客小周发现乘车的里程数超过了5公里,需要支付的费用恰好为46元,起初小周认为系统计算错误,经司机提醒才记起,原来是他有事耽搁没有及时上车,被收取了等待费,则收取的等待费为 元.(直接在横线上写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com