
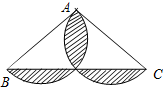
 ∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.
∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.
 过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由; 3°≈0.6;sin53°≈0.8;t
3°≈0.6;sin53°≈0.8;t an74°
an74° 3.5)
3.5)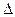 OCD中,
OCD中,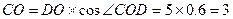 , BO=BC-CO=3.-----------------2分
, BO=BC-CO=3.-----------------2分 -------------------------------------------3分
-------------------------------------------3分 图,过A点作AE⊥BC交BC于E点.若BP = MN,则△BOP≌△MON--------------------------------5分
图,过A点作AE⊥BC交BC于E点.若BP = MN,则△BOP≌△MON--------------------------------5分 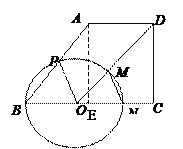
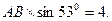 -------------------------------------------------------------------------6分
-------------------------------------------------------------------------6分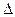 OCD中,
OCD中,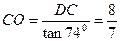 . BO=BC-CO=
. BO=BC-CO=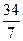
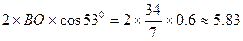
 ⊙O与⊙C外切,CN 取值范围为 0< CN < 6 ------------ 9分
⊙O与⊙C外切,CN 取值范围为 0< CN < 6 ------------ 9分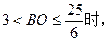 ⊙O与⊙C内切,CN 取值范围为
⊙O与⊙C内切,CN 取值范围为 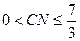 -------------
-------------  10分
10分

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:不详 题型:单选题
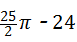
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
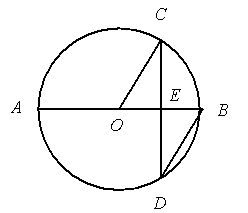
A.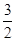 cm cm | B.3 cm | C.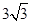 cm cm | D.6cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
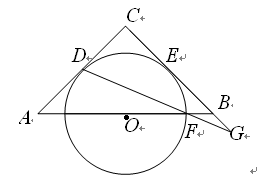
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
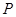 的正上方
的正上方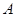 处,从
处,从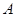 处观测到地球上的最远点
处观测到地球上的最远点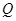 ,若∠
,若∠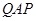 =
= ,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( ) 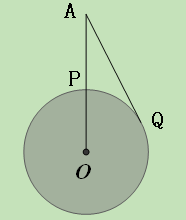
A.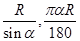 | B. |
C. | D.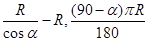 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com