
【题目】已知线段AB=![]() (
(![]() 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含![]() 的代数式表示);
的代数式表示);
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)2AP+CQ-2PQ<1
;(3)2AP+CQ-2PQ<1
【解析】
(1)设AQ=x,BP=y,则CQ=2x,CP=2y.由AB=AQ+CQ+CP+PB= m,得到x+y=![]() ,由PQ=QC+CP=2x+2y即可得到结论;
,由PQ=QC+CP=2x+2y即可得到结论;
(2)分五种情况讨论:①若C在线段AB上;②若C在A的左边;③若C在B的右边;④若B与C重合,⑤若A与C重合.
(3)设AQ=x,BP=y,则CQ=2x,CP=2y.根据(2)得到PQ=![]() ,AP=PQ-AQ=
,AP=PQ-AQ=![]() .
.
代入2AP+CQ-2PQ即可得到结论.
(1)设AQ=x,BP=y,则CQ=2x,CP=2y.
∵AB=AQ+CQ+CP+PB= m,∴x+2x+2y+y=m,∴x+y=![]() ,PQ=QC+CP=2x+2y=2(x+y)=
,PQ=QC+CP=2x+2y=2(x+y)=![]() .
.
(2)分五种情况讨论:
①若C在线段AB上,由(1)可得:PQ=![]() .
.
②若C在A的左边,如图1.

设AQ=x,BP=y,则CQ=2x,CP=2y.
∵AB=CB-CA= (CP+PB)-(CQ+AQ)=m,∴(2y+y)-(x+2x)=m,∴y-x=![]() ,PQ=CP-CQ=2y-2x=2(y-x)=
,PQ=CP-CQ=2y-2x=2(y-x)=![]() .
.
③若C在B的右边,如图2.

设AQ=x,BP=y,则CQ=2x,CP=2y.
∵AB=CA-CB= (CQ+AQ)-(CP+PB) =m,∴(2x+x)-(2y+y)=m,∴x-y=![]() ,PQ= CQ -CP=2x-2y=2(x-y)=
,PQ= CQ -CP=2x-2y=2(x-y)=![]() .
.
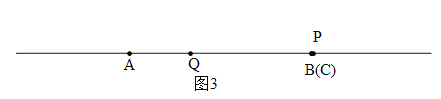
④若B与C重合,则P与B也重合,如图3.
设AQ=x,则CQ=BQ=2x,CP=2BP=0,∴PQ=BQ=2x,AB=3x=m,∴PQ=![]() .
.
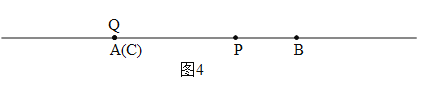
⑤若A与C重合,则Q与A也重合,如图4.
设BP=y,则CQ=AQ=0,CP=2BP=2y,∴PQ=CP=2y,AB=3y=m,∴PQ=![]() .
.
综上所述:点C为直线AB上任一点,则PQ长度为常数![]() .
.
(3)如图1.设AQ=x,BP=y,则CQ=2x,CP=2y.PQ=CP-CQ=2y-2x=2(y-x)=![]() .
.
AP=PQ-AQ=![]() .2AP+CQ-2PQ=
.2AP+CQ-2PQ=![]() =0,∴2AP+CQ-2PQ<1.
=0,∴2AP+CQ-2PQ<1.


科目:初中数学 来源: 题型:
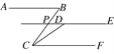
【题目】如图,已知AB∥CF,DE∥CF,DE与BC交于点P,若∠ABC=70°,∠CDE=130°.
(1)试判断∠ABP与∠BPD之间的数量关系,并说明理由;
(2)求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)

查看答案和解析>>
科目:初中数学 来源: 题型:
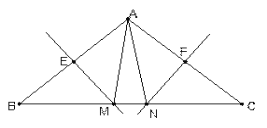
【题目】如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =10cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=2x-4
(1)画出函数的图象;
(2)判断点A(1,-2),B(2,1)是否在该函数的图象上.
(3)已知点A(-2,b)在该函数图像上,求b值;
查看答案和解析>>
科目:初中数学 来源: 题型:
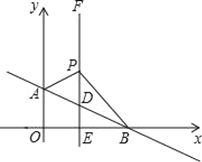
【题目】如图,平面直角坐标系中,直线AB:y=﹣![]() x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
(1)直线AB的表达式为__________________;
(2)①求△ABP的面积(用含n的代数式表示);
②当S△ABP=2时,求点P的坐标;
③在②的条件下,以PB为边在第一象限作等腰直角三角形BPC,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴的正半轴上,且三角形OAB的面积为2,求点A的坐标;
(2)若点A(3,0),BC∥OA,BC=OA,求点C的坐标;
(3)若点A(3,0),点D(3,-4),求四边形ODAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如:![]() ,
,![]() =3.
=3.
(1)仿照以上方法计算:![]() =______;
=______;![]() =_____.
=_____.
(2)若![]() ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次![]()
![]()
![]() =1,这时候结果为1.
=1,这时候结果为1.
(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com