
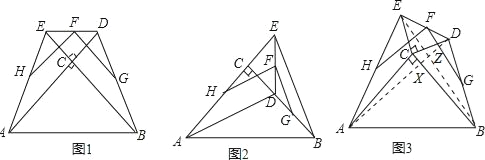
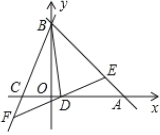
����Ŀ���������ֱ�����ǰ���ABC����DEC��ͼ�ڷţ�������ACB=��DCE=90�㣬F��DE���е㣬H��AE���е㣬G��BD���е㣮
��1����ͼ1������D��E�ֱ���AC��BC���ӳ����ϣ�ͨ���۲�Ͳ���������FH��FG��������ϵΪ______��λ�ù�ϵΪ______��
��2����ͼ2���������ǰ���DEC���ŵ�C˳ʱ����ת��ACE��һ��ֱ����ʱ���������������䣬��1���еIJ����Ƿ���������������֤������������˵�����ɣ�
��3����ͼ3����ͼ1�е���DEC�Ƶ�C˳ʱ����תһ����ǣ��õ�ͼ3����1���еIJ��뻹������ֱ��д�����ۣ�����֤����

���𰸡���1����ȣ���ֱ����2��������֤������������3��������������FH=FG��FH��FG��
��������
������1��֤AD=BE�����������ε���λ���Ƴ�FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE�������Ƴ��𰸣�
BE��FG��BE�������Ƴ��𰸣�
��2��֤��ACD�ա�BCE���Ƴ�AD=BE�����������ε���λ�߶��������Ƴ��𰸣�
��3������BE��AD������ȫ���Ƴ�AD=BE�����������ε���λ�߶��������Ƴ��𰸣�
���������
��1���⣺��CE=CD��AC=BC����ECA=��DCB=90�㣬
��BE=AD��
��F��DE���е㣬H��AE���е㣬G��BD���е㣬
��FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE��
BE��FG��BE��
��FH=FG��
��AD��BE��
��FH��FG��
�ʴ�Ϊ����ȣ���ֱ��
��2���𣺳�����
֤������CE=CD����ECD=��ACD=90�㣬AC=BC��
���ACD�ա�BCE
��AD=BE��
�ɣ�1��֪��FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE��
BE��FG��BE��
��FH=FG��FH��FG��
����1���еIJ��뻹������
��3���𣺳�����������FH=FG��FH��FG��
����AD��BE�����߽���Z��AD��BC��X��
ͬ��1����֤
��FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE��
BE��FG��BE��
��������ECD��ACB�ǵ���ֱ�������Σ�
��CE=CD��AC=BC����ECD=��ACB=90�㣬
���ACD=��BCE��
����ACD����BCE��
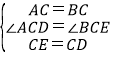 ��
��
���ACD�ա�BCE��
��AD=BE����EBC=��DAC��
�ߡ�DAC+��CXA=90�㣬��CXA=��DXB��
���DXB+��EBC=90�㣬
���EZA=180�㩁90��=90�㣬
��AD��BE��
��FH��AD��FG��BE��
��FH��FG��
��FH=FG��FH��FG��
������FH=FG��FH��FG.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��DE��AC��CE��BD�� 
��1����֤���ı���OCEDΪ���Σ�
��2������AE��BE��AE��BE�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=�� ![]() x2+
x2+ ![]() x+2��ͼ����x�ύ�ڵ�A��B����B�ڵ�A����ࣩ����y�ύ�ڵ�C��������H��0��m����ƽ����x���ֱ��l��ֱ��l����κ���y=��
x+2��ͼ����x�ύ�ڵ�A��B����B�ڵ�A����ࣩ����y�ύ�ڵ�C��������H��0��m����ƽ����x���ֱ��l��ֱ��l����κ���y=�� ![]() x2+
x2+ ![]() x+2��ͼ���ཻ�ڵ�D��E��
x+2��ͼ���ཻ�ڵ�D��E��
��1��д����A����B�����ꣻ
��2����m��0����DEΪֱ������Q������Q��x������ʱ����m��ֵ��
��3��ֱ��l���Ƿ����һ��F��ʹ�á�ACF�ǵ���ֱ�������Σ������ڣ���m��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
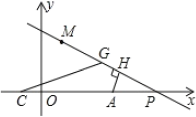
����Ŀ����ͼ��ʾ���ڡ�ABC�У���1����2��G��AD���е㣬�ӳ�BG��AC�ڵ�E��FΪAB��һ�㣬CF��AD��AD�ڵ�H.����˵������AD�ǡ�ABE�Ľ�ƽ���ߣ���BE�ǡ�ABD�ı�AD�ϵ����ߣ���CHΪ��ACD�ı�AD�ϵĸߣ���AH�ǡ�ACF�Ľ�ƽ���ߺ��ߣ�������ȷ����_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������������ͼ����![]() ��
��![]() ���㣬���ڶ����ĵ�
���㣬���ڶ����ĵ�![]() ��
��![]() ������
������![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ����
����![]() �ڵ�������
�ڵ�������
��1������������������ʽ��
��2��������������ͼ��Ľ������ꣻ
��3������![]() ����������������
����������������![]() ��
��![]() �����
��д����![]() ʱ��
ʱ��![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ![]() ����������ɵ������У�
����������ɵ������У�![]() �Ķ�����ڸ���ϣ���
�Ķ�����ڸ���ϣ���![]() ��
��![]() ������ֱ���
������ֱ���![]() ��
��![]() ��
��![]() ����
����![]() ��ԳƵ�ͼ��Ϊ
��ԳƵ�ͼ��Ϊ![]() ��
��
![]() ����
����![]() �����
��д����![]() ������Ϊ________��
������Ϊ________��
![]() �
д��![]() �����Ϊ________��
�����Ϊ________��
![]() ��
��![]() ��
��![]() ���ϣ�ʹ
���ϣ�ʹ![]() ��ֵ��С��д����
��ֵ��С��д����![]() ������Ϊ________��
������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪![]() ��
��![]() �ֱ�Ϊ���������ϵĵ㣬��
�ֱ�Ϊ���������ϵĵ㣬��![]() ��
��![]() ����
����![]() ����
����![]() .
.
��1����![]() ��
��![]() ��
��![]() ��������ꣻ
��������ꣻ
��2����![]() ������
������![]() ��ֱ�߷ֱ�
��ֱ�߷ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����
����![]() ��
��![]() ����ĺ�����ֱ�Ϊ
����ĺ�����ֱ�Ϊ![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
��3����ͼ2����![]() ����
����![]() ��
��![]() ����
����![]() ���Ҳ�һ���㣬
���Ҳ�һ���㣬![]() �ڵ�
�ڵ�![]() ����
����![]() ��ȡ��
��ȡ��![]() ��ʹ
��ʹ![]() ������
������![]() ������
������![]() �ڵ�
�ڵ�![]() �Ҳ��˶�ʱ��
�Ҳ��˶�ʱ��![]() �Ķ����Ƿ�ı�?�����䣬������ֵ�����ı䣬��˵������.
�Ķ����Ƿ�ı�?�����䣬������ֵ�����ı䣬��˵������.
ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��m+3��x+m+1=0��
��1����֤������mȡ��ֵ��ԭ����������������ȵ�ʵ������
��2����x1 �� x2��ԭ���̵���������|x1��x2|=2 ![]() ����m��ֵ���������ʱ���̵�������
����m��ֵ���������ʱ���̵�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com