
|
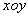 中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在
中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在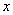 轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为
轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为 ,△POB的面积为
,△POB的面积为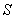 ,
,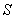 与
与 的函数关系的图象如图2所示,其中四边形ODEF是梯形.
的函数关系的图象如图2所示,其中四边形ODEF是梯形. (1)结合以上信息及图2填空:图2中的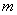 = ;
= ;
(2)求B,C两点的坐标及图2中OF的长;
(3)在图1中,当动点P恰为经过O、C两点的抛物线的顶点时,
①求此抛物线的解析式;
②若点Q在抛物线上,满足以C、P、Q三点为顶点的三角形是直角三角形,求点Q的坐标.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
在平面直角坐标系内,反比例函数和二次函数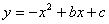 的图象交于点A(m,1)和B(-m,-1)(m≠0).
的图象交于点A(m,1)和B(-m,-1)(m≠0).
(1)当m=2时,分别求反比例函数和二次函数的解析式;
(2)若二次函数的顶点在反比例函数上,求出此时的m值;
(3)当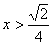 时,这两个函数的增减性一致,请写出满足条件的最小整数m.
时,这两个函数的增减性一致,请写出满足条件的最小整数m.
查看答案和解析>>
科目:初中数学 来源: 题型:
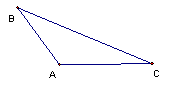
如图,已知:△ABC中,
(1)只用直尺(没有刻度)和圆规求作一点P,使点P同时满足下列两个条件(保留作图痕迹,不必写出作法):①点P到∠CAB的两边距离相等:②点P到A,B两点的距离相等。
(2)若△ABC中,AC = AB = 4,∠CAB=120°,那么请计算以△ABC为轴截面的圆锥的侧面积(保留根号和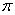 )。
)。
查看答案和解析>>
科目:初中数学 来源: 题型:
(改编)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: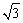 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.(结果精确到0.1米,参考数据:
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.(结果精确到0.1米,参考数据: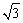 ≈1.732).
≈1.732).
(1)、山坡坡角(即∠ABC)的度数等于 度;
(2)、求A、B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
有如下四个命题:①三角形有且只有一个内切圆;②四边形的内角和与外角和相等;③顺次连接四边形各边中点所得的四边形一定是菱形;④一组对边平行且一组对角相等的四边形是平行四边形.其中的真命题是( )
A.①②③ B.②④ C.①②④ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com