
【题目】现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).(结果精确到0.1m,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192) 
【答案】解:如图,过点A作AP⊥CD于点P,交BC于点Q, 
∵∠CQP=∠AQB,∠CPQ=∠B=90°,
∴∠A=∠C=50°,
在△ABQ中,∵AQ= ![]() =
= ![]() ≈31.10,BQ=ABtanA=20tan50°≈23.84,
≈31.10,BQ=ABtanA=20tan50°≈23.84,
∴CQ=BC﹣BQ=60﹣23.84=36.16,
在△CPQ中,∵PQ=CQsinC=36.16sin50°≈27.70,
∴AP=AQ+PQ=27.70+31.10≈58.8,
答:工件如图摆放时的高度约为58.8cm
【解析】.过点A作AP⊥CD于点P,交BC于点Q,由∠CQP=∠AQB、∠CPQ=∠B=90°知∠A=∠C=50°,在△ABQ中求得分别求得AQ、BQ的长,结合BC知CQ的长,在△CPQ中可得PQ,根据AP=AQ+PQ得出答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( ) 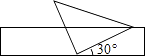
A.3cm
B.6cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图。 
(1)问题 如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证: ![]() .
.
(2)探究 如图,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用 请利用(1)(2)获得的经验解决问题
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以D为圆心,DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数. 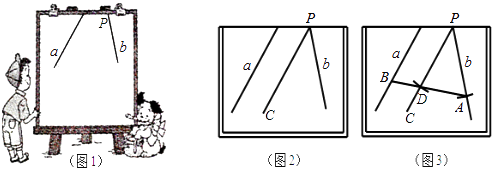
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠CAB=∠B=30°,AB=2 ![]() ,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( )
,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( ) 
A.![]()
B.![]()
C.3﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ![]() ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
A.16
B.15
C.14
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com