
分析 首先把($\sqrt{3}$-2)2005写成($\sqrt{3}$-2)2004($\sqrt{3}$-2)的形式,然后把原式转化为{($\sqrt{3}$+2)($\sqrt{3}$-2)}2004($\sqrt{3}$-2),进而求出结果.
解答 解:($\sqrt{3}$+2)2004($\sqrt{3}$-2)2005
=($\sqrt{3}$+2)2004($\sqrt{3}$-2)2004($\sqrt{3}$-2)
={($\sqrt{3}$+2)($\sqrt{3}$-2)}2004($\sqrt{3}$-2)
={($\sqrt{3}$)2-4}2004($\sqrt{3}$-2)
=(3-4)2004($\sqrt{3}$-2)
=(-1)2004($\sqrt{3}$-2)
=$\sqrt{3}$-2.
点评 本题主要考查了二次根式的混合运算的知识,解答本题的关键是先把($\sqrt{3}$-2)2005写成($\sqrt{3}$-2)2004($\sqrt{3}$-2)的形式,此题难度不大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
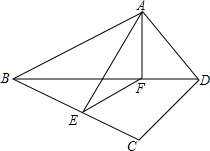 已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.
已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图.在边长为2的菱形ABCD中,∠A=60°,点P为射线AB上一个动点.过点P作PE⊥AB交射线AD于点E.将△AEP沿直线PE折叠,点A的对应点为F,连接FD、FC,若△FDC为直角三角形时,AP的长为$\frac{1}{2}$或$\frac{3}{2}$.
如图.在边长为2的菱形ABCD中,∠A=60°,点P为射线AB上一个动点.过点P作PE⊥AB交射线AD于点E.将△AEP沿直线PE折叠,点A的对应点为F,连接FD、FC,若△FDC为直角三角形时,AP的长为$\frac{1}{2}$或$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com