
(本题10分)问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
 探索研究
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
|
x |
…… |
|
|
|
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |

|
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过
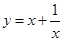
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
科目:初中数学 来源: 题型:
(本题10分)问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
![]() 探索研究
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x | …… |
|
|
| 1 | 2 | 3 | 4 | …… |
| y | …… |
|
|
|
|
|
|
| …… |

|
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过
![]()
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
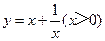
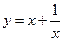
| x | …… | 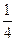 | 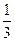 | 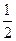 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
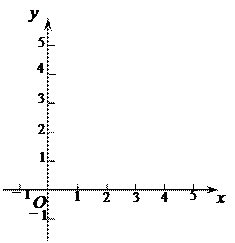
|
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(浙江金华卷)数学 题型:解答题
(本题10分)某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路 程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型:解答题
(本题10分)问题情境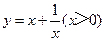

已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
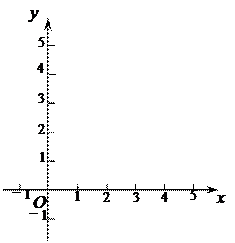
①填写下表,画出函数的图象:
| x | …… |  | 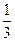 | 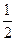 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com