
【题目】在平面直角坐标系中,O为坐标原点,过二次函数y=﹣x2+4x图象上的点A(3,3)作x轴的垂线交x轴于点B.
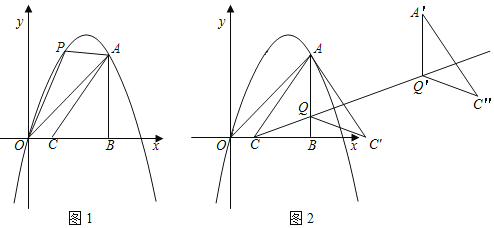
(1)如图1,P为线段OA上方抛物线上的一点,在x轴上取点C(1,0),点M、N为y轴上的两个动点,点M在点N的上方且MN=1.连接AC,当四边形PACO的面积最大时,求PM+MN![]() NO的最小值.
NO的最小值.
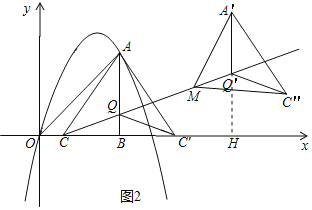
(2)如图2,点Q(3,1)在线段AB上,作射线CQ,将△AQC沿直线AB翻折,C点的对应点为C',将△AQC'沿射线CQ平移3![]() 个单位得△A'Q'C″,在射线CQ上取一点M,使得以A'、M、C″为顶点的三角形是等腰三角形,求M点的坐标.
个单位得△A'Q'C″,在射线CQ上取一点M,使得以A'、M、C″为顶点的三角形是等腰三角形,求M点的坐标.
【答案】(1)最小值为![]() ;(2)点M坐标为(7,3),(
;(2)点M坐标为(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() )
)
【解析】
(1)把四边形PACO沿OA分成△OAP与△OAC,由于△OAC三边确定,面积为定值,故△OAP面积最大时四边形面积也最大.过点P作x轴垂线交OA于D,设点P横坐标为t,则能用t表示PD的长,进而得到△OAP关于t的二次函数关系式,用公式法可求得t![]() 时△OAP面积最大,即求得此时点P坐标.把点P向下平移1个单位得P',易证四边形MNP'P是平行四边形,所以PM=P'N.过点O作经过第二、四象限的直线l,并使直线l与x轴夹角为60°,过点N作NG⊥直线l于点G,则由30°角所对直角边等于斜边一半可知NG
时△OAP面积最大,即求得此时点P坐标.把点P向下平移1个单位得P',易证四边形MNP'P是平行四边形,所以PM=P'N.过点O作经过第二、四象限的直线l,并使直线l与x轴夹角为60°,过点N作NG⊥直线l于点G,则由30°角所对直角边等于斜边一半可知NG![]() NO.所以PM+MN
NO.所以PM+MN![]() NO可转化为P'N+NG+1,易得当点P'、N、G在同一直线上最小.把PD延长交直线l于点F,构造特殊Rt△P'FG和Rt△OEF,利用点P坐标和30°、60°的三角函数即可求得P'G的长.
NO可转化为P'N+NG+1,易得当点P'、N、G在同一直线上最小.把PD延长交直线l于点F,构造特殊Rt△P'FG和Rt△OEF,利用点P坐标和30°、60°的三角函数即可求得P'G的长.
(2)由点B、C、Q的坐标求CQ的长和点C'坐标;过点Q'作x轴的垂线段Q'H,易证△CBQ∽△CHQ',故有![]() ,求得CH、HQ'的长即求得点Q'坐标,进而得到向右向上平移的距离,求得点A'、C'的坐标.求直线CQ解析式,设CQ上的点M横坐标为m,用两点间距离公式可得用m表示A'M和C'M的长.因为△A'MC'是等腰三角形,分三种情况讨论,得到关于m的方程,求解即求得相应的m的值,进而得点M坐标.
,求得CH、HQ'的长即求得点Q'坐标,进而得到向右向上平移的距离,求得点A'、C'的坐标.求直线CQ解析式,设CQ上的点M横坐标为m,用两点间距离公式可得用m表示A'M和C'M的长.因为△A'MC'是等腰三角形,分三种情况讨论,得到关于m的方程,求解即求得相应的m的值,进而得点M坐标.
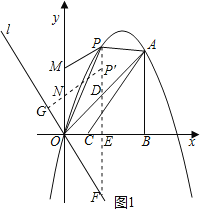
(1)如图1,过点O作直线l,使直线l经过第二、四象限且与x轴夹角为60°;
过点P作PF⊥x轴于点E,交OA于点D,交直线l于点F;在PF上截取PP'=1;过点N作NG⊥直线l于点G
∵A(3,3),AB⊥x轴于点B
∴直线OA解析式为y=x,OB=AB=3
∵C(1,0)
∴S△AOC![]() OCAB
OCAB![]() 1×3
1×3![]() ,是定值
,是定值
设P(t,﹣t2+4t)(0<t<3)
∴D(t,t)
∴PD=﹣t2+4t﹣t=﹣t2+3t
∴S△OAP=S△OPD+S△APD![]() PDOE
PDOE![]() PDBE
PDBE![]() PDOB
PDOB![]() (t2﹣3t)
(t2﹣3t)
∴t![]() 时,S△OAP最大
时,S△OAP最大
此时,S四边形PACO=S△AOC+S△OAP最大
yP=﹣(![]() )2+3
)2+3![]()
∴P(![]() ,
,![]() )
)
∴P'E=PE﹣PP'![]() 1
1![]() ,即P'(
,即P'(![]() ,
,![]() )
)
∵点M、N在y轴上且MN=1
∴PP'=MN,PP'∥MN
∴四边形MNP'P是平行四边形
∴PM=P'N
∵∠NGO=90°,∠NOG=90°﹣60°=30°
∴Rt△ONG中,NG![]() NO
NO
∴PM+MN![]() NO=P'N+NG+1
NO=P'N+NG+1
∴当点P'、N、G在同一直线上,即P'G⊥直线l时,PM+MN![]() NO=P'G+1最小
NO=P'G+1最小
∵OE![]() ,∠EOF=60°,∠OEF=90°
,∠EOF=60°,∠OEF=90°
∴Rt△OEF中,∠OFE=30°,tan∠EOF![]()
∴EF![]() OE
OE![]()
∴P'F=P'E+EF![]()
∴Rt△P'GF中,P'G![]() P'F
P'F![]()
∴P'G+1![]() 1
1![]()
∴PM+MN![]() NO的最小值为
NO的最小值为![]()
(2)延长A'Q'交x轴于点H
∵C(1,0),Q(3,1),QB⊥x轴于点B
∴CB=2,BQ=1
∴CQ![]()
∵△AQC沿直线AB翻折得△AQC'
∴B(3,0)是CC'的中点
∴C'(5,0)
∵平移距离QQ'=3![]()
∴CQ'=CQ+QQ'=4![]()
∵QB∥Q'H
∴△CBQ∽△CHQ'
∴![]()
∴CH=4CB=8,yQ'=HQ'=4BQ=4
∴xQ'=OC+CH=1+8=9
∴Q'(9,4)
∴点Q(3,1)向右平移6个单位,向上平移3个单位得到点Q'(9,4)
∴A'(9,6),C'(11,3)
∴A'C'![]()
设直线CQ解析式为y=kx+b
∴![]() 解得:
解得: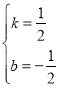
∴直线CQ:y![]() x
x![]()
设射线CQ上的点M(m,![]() m
m![]() )(m>1)
)(m>1)
∴A'M2=(9﹣m)2+(6![]() m
m![]() )2=(9﹣m)2+(
)2=(9﹣m)2+(![]() m)2
m)2
C'M2=(11﹣m)2+(3![]() m
m![]() )2=(11﹣m)2+(
)2=(11﹣m)2+(![]() m)2
m)2
∵△A'MC'是等腰三角形
①若A'M=A'C',则(9﹣m)2+(![]() m)2=13
m)2=13
解得:m1=7,m2![]()
∴M(7,3)或(![]() ,
,![]() )
)
②若C'M=A'C',则(11﹣m)2+(![]() m)2=13
m)2=13
解得:m1![]() ,m2=13
,m2=13
∴M(![]() ,
,![]() )或(13,6)
)或(13,6)
③若A'M=C'M,则(9﹣m)2+(![]() m)2=(11﹣m)2+(
m)2=(11﹣m)2+(![]() m)2
m)2
解得:m=10
∴M(10,![]() )
)
综上所述,点M坐标为(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
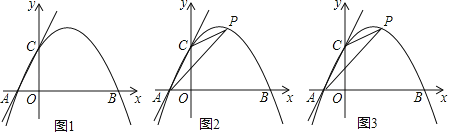
【题目】平面直角坐标系中,点O是坐标原点,抛物线y=ax2+![]() x+c与x轴交于A、B两点,点B的坐标为(4,0),与y轴交于点C,直线y=kx+2经过A、C两点.
x+c与x轴交于A、B两点,点B的坐标为(4,0),与y轴交于点C,直线y=kx+2经过A、C两点.
(1)如图1,求a、c的值;
(2)如图2,点P为抛物线y=ax2+![]() x+c在第一象限的图象上一点,连接AP、CP,设点P的橫坐标为t,△ACP的面积为S,求S与t的函数解析式,并直接写出自变量t的取值范围;
x+c在第一象限的图象上一点,连接AP、CP,设点P的橫坐标为t,△ACP的面积为S,求S与t的函数解析式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,点D为线段AC上一点,直线OD与直线BC交于点E,点F是直线OD上一点,连接BP、BF、PF、PD,BF=BP,∠FBP=90°,若OE=![]() ,求直线PD的解析式.
,求直线PD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
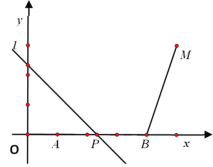
【题目】如图,点A(1, 0)、B(4,0)、M(5,3).动点P从A点出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线l:y= -x+b也随之移动.设移动时间为t秒.
(1)当t=1时,求直线l的解析式.
(2)若直线l与线段BM有公共点,求t的取值范围.
(3)当点M关于直线l的对称点落在坐标轴上时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校A班和B班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
A班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
18 11 22 25 25 18 27 25 22 27
B班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据:
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 23 | 30 | 30 | 59.7 |
B班的同学还将自主复习时间分为四大类:第一类为时间小于10分钟以下;第二类为时间大于或等于10分钟且小于20分钟;第三类为时间大于或等于20分钟且小于30分钟;第四类为时间大于或等于30分钟,并得到如下的扇形图.
(1)在扇形图中,第一类所对的圆心角度数为 .
(2)写出A班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 25 | 16 |
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些.其理由为(至少两条): .

查看答案和解析>>
科目:初中数学 来源: 题型:
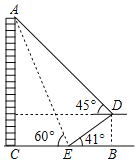
【题目】郑州大学(ZhengzhouUniversity),简称“郑大”,是中华人民共和国教育部与河南省人民政府共建的全国重点大学,首批“双一流”世界一流大学、“211工程”.某学校兴趣小组3人来到郑州大学门口进行测量,如图,在大楼AC的正前方有一个舞台,舞台前的斜坡DE=4米,坡角∠DEB=41°,小红在斜坡下的点E处测得楼顶A的仰角为60°,在斜坡上的点D处测得楼顶A的仰角为45°,其中点B,C,E在同一直线上求大楼AC的高度.(结果精确到整数.参考数据:![]() ≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)
≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)
查看答案和解析>>
科目:初中数学 来源: 题型:
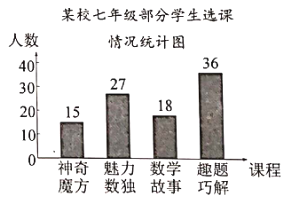
【题目】为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图.根据统计图,请估计该校七年级720名学生选“数学故事”的人数.
(2)学校将“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”.已知小聪不在A班,求他与小慧被分到同一个班的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
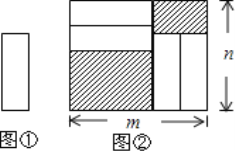
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com