
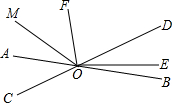
 如图,直线AB,CD相交于点O,∠DOE:∠BOE=3:1,OF平分∠AOD,
如图,直线AB,CD相交于点O,∠DOE:∠BOE=3:1,OF平分∠AOD,分析 (1)根据对顶角相等,以及邻补角的定义,可得关于∠AOC、∠AOF的方程组,解方程可求∠EOF;
(2)根据角平分线的定义和已知条件可得∠MOE是平角的$\frac{3}{4}$,从而得到∠MOE的度数.
解答 解:(1)依题意有:
$\left\{\begin{array}{l}{∠AOC+2∠AOF=180°}\\{∠AOC=∠AOF-30°}\end{array}\right.$,
解得$\left\{\begin{array}{l}{∠AOF=70°}\\{∠AOC=40°}\end{array}\right.$,
∵∠BOD=∠AOC=40°,∠DOE:∠BOE=3:1,
∴∠DOE=30°,
∴∠EOF=∠DOE+∠DOF=∠DOE+∠AOF=100°;
(2)∵射线OM平分∠AOF,
∴∠AOM=$\frac{1}{2}$∠AOF,
∵OF平分∠AOD,
∴∠AOF=$\frac{1}{2}$∠AOD,
∴∠AOM=$\frac{1}{4}$∠AOD,
∵∠DOE:∠BOE=3:1,
∴∠MOD=$\frac{3}{4}$∠AOD,∠DOE=$\frac{3}{4}$∠DOB,
∴∠MOE=∠MOD+∠DOE=$\frac{3}{4}$∠AOD+$\frac{3}{4}$∠DOB=$\frac{3}{4}$(∠AOD+∠DOB)=$\frac{3}{4}$∠AOB,
∴∠MOE的度数为180°×$\frac{3}{4}$=135°.
点评 本题考查了角平分线的定义,对顶角相等以及邻补角的定义,关键是方程思想的运用.


科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD=BC | B. | AB∥CD,AB=CD | C. | AD∥BC,AB=CD | D. | AB∥CD,AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
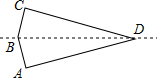 如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°,将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为2的平行四边形,则BC=2或1.
如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°,将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为2的平行四边形,则BC=2或1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
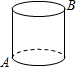 如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蚂蚁,想吃到与A点相对的上底面B处的一只已被粘住的苍蝇,这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点,则最短路程是10$\sqrt{4+{π}^{2}}$cm.(结果用根号表示)
如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蚂蚁,想吃到与A点相对的上底面B处的一只已被粘住的苍蝇,这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点,则最短路程是10$\sqrt{4+{π}^{2}}$cm.(结果用根号表示)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
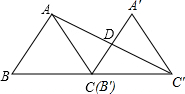 如图,已知三角形ABC的面积为12,将三角形ABC沿BC平移到三角形A′B′C′,使B′和C重合,连接AC′交A′C于D,D是A′C的中点,则三角形C′DC的面积为6.
如图,已知三角形ABC的面积为12,将三角形ABC沿BC平移到三角形A′B′C′,使B′和C重合,连接AC′交A′C于D,D是A′C的中点,则三角形C′DC的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com