
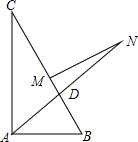
 在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 10 |
分析 作NE⊥AB于E,NF⊥AC于F,连接NC,NB,根据角平分线的性质得到NF=NE,根据线段的垂直平分线的性质得到NC=NB,证明Rt△NFC≌Rt△NEB,得到CF=BE,求出BE的长,根据勾股定理计算即可.
解答 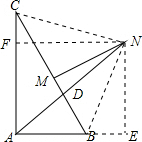 解:作NE⊥AB于E,NF⊥AC于F,连接NC,NB,
解:作NE⊥AB于E,NF⊥AC于F,连接NC,NB,
∵AD是∠A的角平分线,
∴NE=NF,
∵MN是边BC的垂直平分线,
∴NC=NB,
在Rt△NFC和Rt△NEB中,
$\left\{\begin{array}{l}{NC=NB}\\{NF=NE}\end{array}\right.$,
∴Rt△NFC≌Rt△NEB,
∴CF=BE,
∵6+BE=8-CF,
∴CF=BE=1,∴NE=AF=7,
由勾股定理得,NB=$\sqrt{B{E}^{2}+N{E}^{2}}$=5$\sqrt{2}$,
∵∠A为直角,AB=6,AC=8,
∴BC=10,则NB=5,
∴MN=5,
故选:C.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
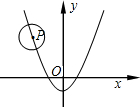 如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com