
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
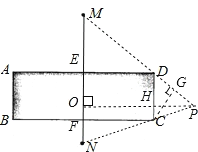
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

【答案】![]()
【解析】
据已知首先得出DH=HP=x米,NO=(20![]() +40-x)米,PO=(60+x)米,再利用平行线分线段成比例定理和三角形面积求出即可.
+40-x)米,PO=(60+x)米,再利用平行线分线段成比例定理和三角形面积求出即可.
连接MD并延长,连接NC并延长,使其两延长线相交于点P,
作PO⊥MN于O,作CG⊥MP于G,
根据题意可得出:
ME=60,DE=HO=FC=60米,FN=20![]() 米,EF=40,
米,EF=40,
∴NC=![]() ,
,
=40![]() 米,
米,
设EO=x米,
∴DH=x米,
∵ME=DE=60米,
∴∠MDE=45,
∴DH=HP=x米,NO=(20![]() +40x)米,PO=(60+x)米,
+40x)米,PO=(60+x)米,
∵FC∥PO,
∴![]() ,
,
∴x![]() ,
,
解得:x=6020![]() ,
,
∴PO=(12020![]() )米,NO=(40
)米,NO=(40![]() 20)米,
20)米,
![]() CDHP=
CDHP=![]() DPCG,
DPCG,
![]() ×40×(12020
×40×(12020![]() 60)=
60)= ![]() ×
×![]() [20
[20![]() +40(40
+40(40![]() 20)]CG,
20)]CG,
CG=20![]() 米,
米,
∴行走的最短距离长为:NC+CG=(40![]() +20
+20![]() )米.
)米.
故答案为:40![]() +20
+20![]()


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.

(1)请画出此时小丽在阳光下的影子;
(2)若已知小明的身高为1.60 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
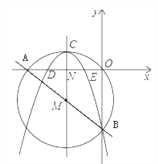
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
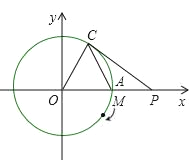
【题目】如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
(1)求∠AOC的度数;
(2)P为x轴正半轴上一点,且PA=OA,连接PC,试判断PC与⊙O的位置关系,并说明理由;
(3)有一动点M从A点出发,在⊙O上按顺时针方向运动一周,当S△MAO=S△CAO时,求动点M所经过的弧长,并写出此时M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
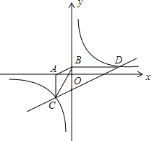
【题目】如图,已知双曲线![]() 经过点
经过点![]() ,点
,点![]() 是双曲线第三象限分支上的动点,过点
是双曲线第三象限分支上的动点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
![]() 求
求![]() 的值;
的值;
![]() 若
若![]() 的面积为
的面积为![]() ,
,
①若直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 、
、![]() 的值;
的值;
②根据图象,直接写出![]() 时
时![]() 的取值范围;
的取值范围;
③判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
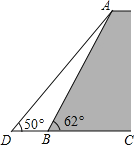
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是_____
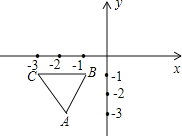
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行八年级“生活中的数学知识”竞赛活动,甲、乙两校分别派五名同学参加竞赛,其成绩分别是(单位:分):甲校五名同学:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;乙校五名同学:
;乙校五名同学:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .根据以上数据解答下列问题:
.根据以上数据解答下列问题:
![]() 把表格空格填完整:
把表格空格填完整:
学校 | 平均数(分) | 中位数(分) | 众数(分) |
甲校五位同学 | ________ |
| ________ |
乙校五位同学 |
| ________ |
|
![]() 根据上述数据,请你分析哪所学校同学的竞赛成绩相对较好?
根据上述数据,请你分析哪所学校同学的竞赛成绩相对较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
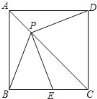
【题目】如图,![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 对角线
对角线![]() 上一动点(
上一动点(![]() 与
与![]() 、
、![]() 不重合),点
不重合),点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
![]() 求证:①
求证:①![]() ;②
;②![]() ;
;
![]() 设
设![]() ,
,![]() 的面积为
的面积为![]() .
.
①求出![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 取何值时,
取何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com