
【题目】如图,若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且两条直线与
,且两条直线与![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ;那么
;那么![]() 的面积为____.
的面积为____.

【答案】![]()
【解析】
根据B点在直线y=2x+1上,且横坐标为1,求出B点的坐标,将B点的坐标代入直线y=kx+4的解析式,即可求出直线AB的解析式,再根据直线y=2x+1和直线y=x+4求得与y轴交点点A和点C的坐标,再根据三角形的面积公式得出S△ABC.
解:∵B点在直线y=2x+1上,且横坐标为1,
∴y=2×(1)+1=3,即B点的坐标为(1,3)
将(1,3)代入直线y=kx+4得:3=k+4,
解得k=1;
∴直线AB的解析式为y=x+4,
∴直线AB与y轴交点A的坐标为(0,4),
∵直线y=2x+1与y轴交点C的坐标为(0,1),
∴AC=41=3,
∴S△ABC=![]() ×3×1=
×3×1=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的二元一次方程组x-y=3a①和x+3y=4-a②.
(1)如果![]() 是方程①的解,求a的值;
是方程①的解,求a的值;
(2)当a=1时,求两个方程的公共解;
(3)若方程组![]() 的解满足x≤0,求y的取值范围.
的解满足x≤0,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中,有A,O,B,C,D,E,F,H,G九个格点.抛物线l的解析式为y=![]() x2+bx+c.
x2+bx+c.
(1)若l经过点O(0,0)和B(1,0),则b= ,c= ;它还经过的另一格点的坐标为 .
(2)若l经过点H(﹣1,1)和G(0,1),求它的解析式及顶点坐标;通过计算说明点D(1,2)是否在l上.
(3)若l经过这九个格点中的三个,直接写出所有满足这样的抛物线的条数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,四边形![]() 为矩形,如图1,
为矩形,如图1,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,已知
,已知![]() 满足
满足![]() .
.

(1)求![]() 的值;
的值;
(2)①如图1,![]() 分别为
分别为![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() ;
;
②如图2,![]() 分别为
分别为![]() 上一点,
上一点,![]() 交于点
交于点![]() . 若
. 若![]() ,
,![]() ,则
,则![]() ___________
___________
(3)如图3,在矩形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上且
上且![]() ,连接
,连接![]() ,动点
,动点![]() 在线段
在线段![]() 是(动点
是(动点![]() 与
与![]() 不重合),动点
不重合),动点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于
于![]() . 试问:当
. 试问:当![]() 在移动过程中,线段
在移动过程中,线段![]() 的长度是否发生变化?若不变求出线段
的长度是否发生变化?若不变求出线段![]() 的长度;若变化,请说明理由.
的长度;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.
的图象与性质.
因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … |
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 |
|
| 1 |
|
| … |
| … |
|
| 2 | 3 | 5 |
|
| 0 |
|
| … |
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示).
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③![]() 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 、
、![]() 、
、![]() 不在同一条直线上,
不在同一条直线上,![]() .
.

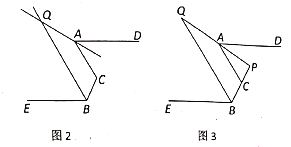
(1)如图1,当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图2,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图3,在(2)的前提下,有![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com