【题目】不等式5﹣x＞2的解集是（ ）
A.x＜3
B.x＞3
C.x＜﹣7
D.x＞﹣3
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图乙，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，点P为射线BD，CE的交点．
（1）如图甲，将△ADE绕点A 旋转，当C、D、E在同一条直线上时，连接BD、BE，则下列给出的四个结论中，其中正确的是 .
①
②
③
④
（2）若AB=4，AD=2，把△ADE绕点A旋转，
①当∠EAC=90°时，求PB的长；
②求旋转过程中线段PB长的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅统计图．
请根据图中的信息，回答下列问题：
（1）这次抽样调查中共调查了 人；
（2）请补全条形统计图；
（3）扇形统计图中18﹣23岁部分的圆心角的度数是 ；
（4）据报道，目前我国12﹣35岁网瘾人数约为2000万，请估计其中12﹣23岁的人数
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，OA，OD是⊙O半径．过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B．
(1)求证：直线CD是⊙O的切线；
(2)如果D点是BC的中点，⊙O的半径为 3cm，求
的长度．(结果保留π)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，△ABC的三条边BC＝
，CA＝
，AB＝
，D为△ABC内一点，且∠ADB＝∠BDC＝∠CDA＝120°，DA＝
，DB＝
，DC＝
．
（1）若∠CDB＝18°，则∠BCD＝ °；
（2）将△ACD绕点Ａ顺时针方向旋转90°到
，画出
，若∠CAD＝20°，求
度数；
（3）试画出符合下列条件的正三角形：M为正三角形内的一点，M到正三角形三个顶点的距离分别为
、
、
，且正三角形的边长为
＋
＋
，并给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠AOB=120°，OC、OD过点O的射线，射线OM、ON分别平分∠AOC和∠DOB．
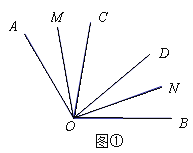
（1）如图①，若OC、OD是∠AOB 的三等分线，求∠MON的度数；
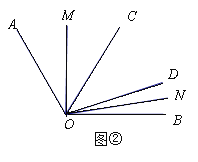
（2）如图②，若∠COD=50°，∠AOC≠∠DOB，则∠MON= °；
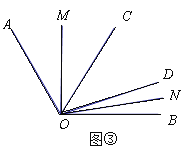
（3）如图③，在∠AOB内，若∠COD=α（0°<α<60°），则∠MON= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
