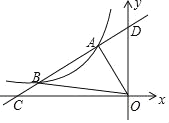
【题目】如图，直线y＝kx+b与反比例函数
的图象分别交于点A（﹣1，2），点B（﹣4，n），与x轴，y轴分别交于点C，D．
（1）求此一次函数和反比例函数的解析式；
（2）求△AOB的面积．
【答案】（1）y=
x+
；（2）
【解析】
（1）先根据点A求出k值，再根据反比例函数解析式求出n值，利用待定系数法求一次函数的解析式；
（2）利用三角形的面积差求解．S△AOB=S△AOC﹣S△BOC=5
．
解：（1）将点A（﹣1，2）代入
中，2=
；
∴m=﹣2．
∴反比例函数解析式为y=﹣
．
将B（﹣4，n）代入y=﹣中，n=﹣
；
∴n=．
∴B点坐标为（﹣4，）．
将A（﹣1，2）、B（﹣4，）的坐标分别代入y=kx+b中，
得
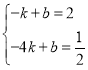，解得
．
∴一次函数的解析式为y=x+；
（2）当y=0时，x+=0，x=﹣5；
∴C点坐标（﹣5，0），∴OC=5．
S△AOC=OC|yA|=×5×2=5．
S△BOC=OC|yB|=×5×
．
S△AOB=S△AOC﹣S△BOC=5．
科目：初中数学 来源： 题型：
【题目】等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD的中点，连接MN、NF．
问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为 ，线段MN和线段NF的数量关系为 ；
深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；
拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从﹣1，﹣2，﹣3，﹣4，﹣5，﹣6中任取一个数作为k的值，则能使分式方程
有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为（ ）
A.
B.
C.
D.0
查看答案和解析>>
科目：初中数学 来源： 题型：
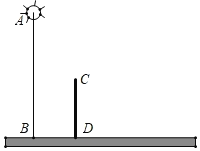
【题目】如图所示，灯在距地面6米的A处，与灯柱AB相距3米的地方有一长3米的木棒CD直立于地面．
（1）在图中画出木棒CD的影子，并求出它的长度；
（2）当木棒绕其与地面的固定端点D按顺时针方向旋转到地面时，其影子的变化有什么规律？你能求出其影长的取值范围吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
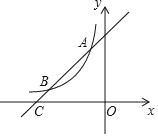
【题目】如图，一次函数y＝x+4的图象与反比例函数y＝
(k为常数且k≠0)的图象交于A(﹣1，a)，B两点，与x轴交于点C．
(1)求a，k的值及点B的坐标；
(2)若点P在x轴上，且S△ACP＝
S△BOC，直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
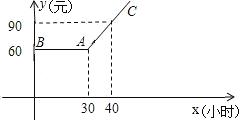
【题目】某市推出电脑上网包月制，每月收取费用y（元）与上网时间x（小时）的函数关系如图所示，其中BA是线段，且BA∥x轴，AC是射线．
（1）当x≥30，求y与x之间的函数关系式；
（2）若小李4月份上网20小时，他应付多少元的上网费用？
（3）若小李5月份上网费用为75元，则他在该月份的上网时间是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
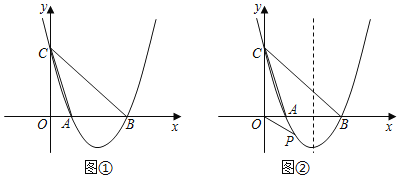
【题目】如图①，已知抛物线y＝ax2﹣4amx+3am2（a、m为参数，且a＞0，m＞0）与x轴交于A、B两点（A在B的左边），与y轴交于点C．
（1）求点B的坐标（结果可以含参数m）；
（2）连接CA、CB，若C（0，3m），求tan∠ACB的值；
（3）如图②，在（2）的条件下，抛物线的对称轴为直线l：x＝2，点P是抛物线上的一个动点，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的的等腰直角三角形．若存在，求出所有符合条件的点P的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019年春节，小娜家购买了4个灯笼，灯笼上分别写有“欢”、“度”、“春”、“节”（外观完全一样）．
（1）小娜抽到“2019年”是 事件，“欢”字被抽中的是 事件；（填“不可能”或“必然”或“随机”）．小娜从四个灯笼中任取一个，取到“春”的概率是 ．
（2）小娜从四个灯笼中先后取出两个灯笼，请用列表法或画树状图法求小娜恰好取到“春”、“节”两个灯笼的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com